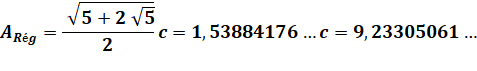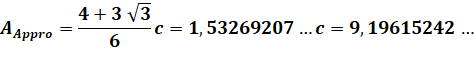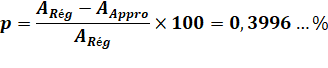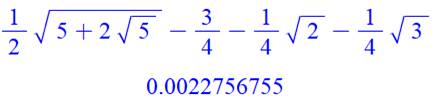|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PENTAGONE RÉGULIER Constructions approchées étonnantes
! D'abord
une construction médiévale particulièrement simple. Puis,
deux constructions tout aussi simples proposées par Ian, à partir d'un triangle
équilatéral implanté dans un carré.
Précision 4 et 3 pour mille. La
construction suivante, tout aussi étonnante, m'a été proposée par Jean-Louis
Breuil. Il s'agit d'une construction inattendue mêlant carré,
triangles
équilatéraux et bissectrice.
|
Voir La construction exacte / Approchée
de Dürer
|
|
||||||||
|
Pour
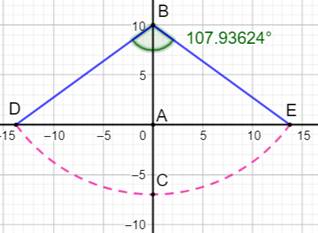
commencer, une construction approchée particulièrement simple à réaliser. Construction de l'angle
Approximation
|
BA = 10 BD = 17 |
|||||||
|
Construction approchée du pentagone
pour géomètre ou arpenteur
Un agrandissement montre le pentagone
régulier en pointillés bleus. L'écart entre les deux points est inférieure à
1 mm pour une hauteur du pentagone de 25 cm.
|
|
|||||||
Voir Angles en
Pi / 5 / Construction approchée
avec arctan(3) voisin de 72 °
|
|
|||
|
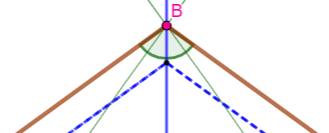
Une
construction approchée particulièrement simple à réaliser au prix d'une trisection. Construction approchée du pentagone
pour géomètre ou arpenteur
Figure Pentagone approché en bleu. Pentagone régulier en pointillés roses, à peine
visible à la pointe supérieure. |
|
||
|
Longueur la hauteur verticale en pointillés pour
chacun des pentagones. |
|
||
|
Précision de 0,4 % |
|
||
Voir Nombres en
1,53… / Brève
664
|
Une autre
construction approchée très simple.
Précision du même ordre que la construction qui suit, basée sur un principe analogue. |
|
Merci à Ian Mansour de Grange pour ces petites
"cerises", comme il appelle ces constructions
|
|
||
|
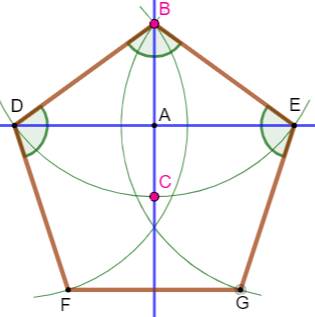
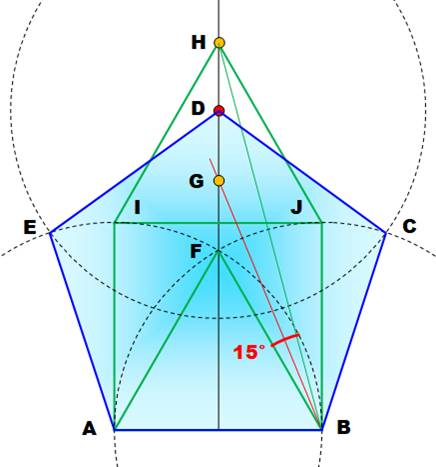
Étapes de construction du pentagone
régulier ABCDE
|
|
|
|
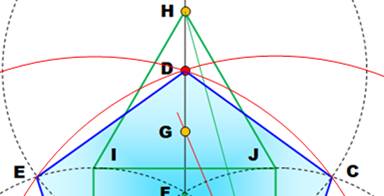
Note La construction exacte
du pentagone selon ce type de méthode est très proche. En
effet Point D exact
= intersection des cercles (B, BE) et (A, AC) Cercles en
rouge qui se croisent sur le point D de la figure. Il faudrait grossir
beaucoup pour observer la différence. |
|
|
|
Repérez les deux losanges verts: AFHI et BFHJ. Losanges
car quatre côtés égaux: BF = BJ = HJ = HF qui sont aussi égaux à AB = 1. L'angle au sommet du losange (30°) est partagé en
deux angles de 15° par la diagonale du
losange. À son tour la bissectrice BG (en rouge) partage l'un d'eux en deux
angles de 7,5°. L'angle ABG vaut 60 + 7,5 = 67,5° = 3Pi/8 radians. Sa
tangente vaut 1 + racine de 2. |
Voir Angles
en pi/8 – Calcul des lignes trigonométriques / Angles – Index
|
|
||||
|
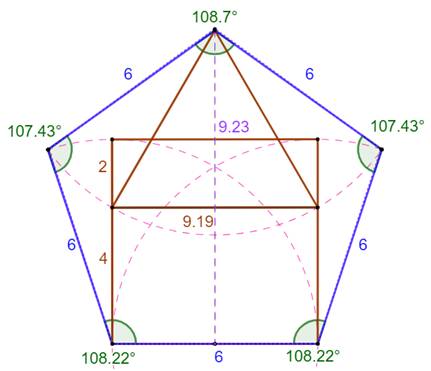
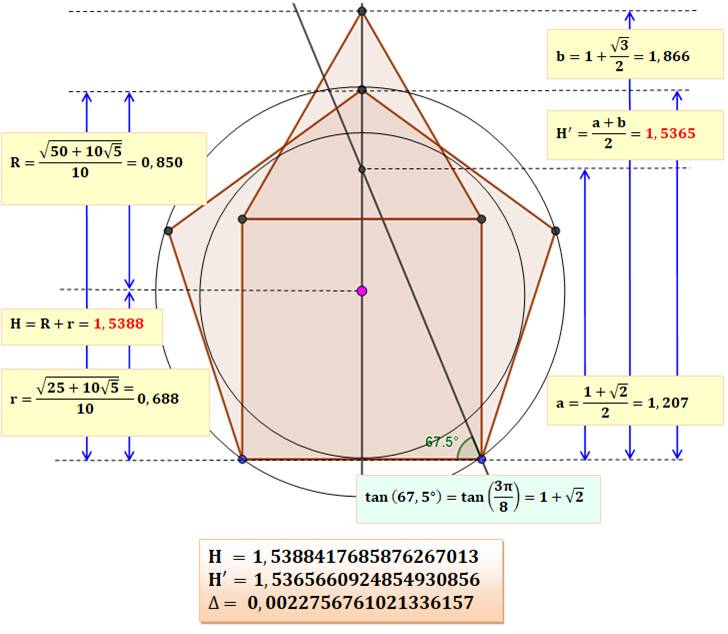
Évaluation de la hauteur du
pentagone De ce côté (à gauche), la
hauteur H du pentagone vaut: H = 1, 5388 … à comparer à la
hauteur de la figure H'. Un écart de 0,00227, soit 0,15%. |
Évaluation de la hauteur de la
figure construite
|
|||
|
|
||||
|
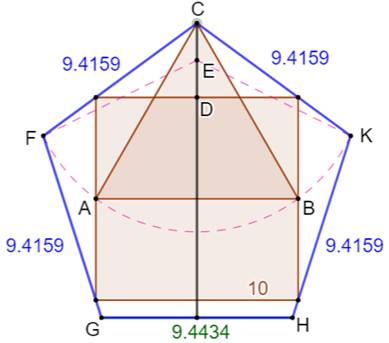
Construction avec GeoGebra |
Valeurs relevées
|
Comparaison e est la hauteur du pentagone. f1 et g1 sont les hauteurs aux points G et H Le point milieu est à la hauteur
(demi-somme): 9,2196 À comparer à 9,2333 Écart: 0,1366, soit 0,15 %. |
||
|
Formule exprimant
la différence |
|
|||
Merci à Jean-Louis Breuil
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/PentaCur.htm
|
![]()