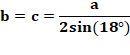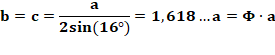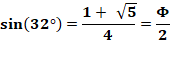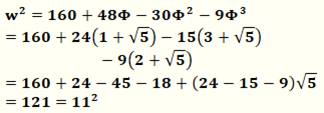|
Édition du: 22/01/2021 |
|
INDEX |
Topologie – Graphes |
|||||
![]()
|
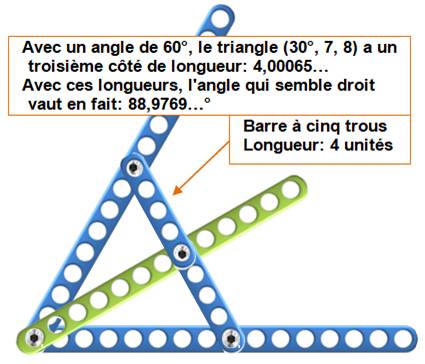
GRAPHES RIGIGES Polygones rigides façon Meccano
Ici, on prolonge
le défi en créant des structures polygonales rigides avec des barres de
Meccano. Dit autrement, on cherche des longueurs de barre en nombres
entiers. D'une manière
générale Gerard ’t Hooft
a développé toute une géométrie
utilisant ces barres (bissectrice, trisectrice, rapport, polygones, etc.). |
||
|
|
Sommaire de cette page >>> Approche >>> Étude du pentagone >>> Étude du pentagone – Suite >>> Exemple de montage avec l'octogone |
Débutants Glossaire |
|
Rigide L'utilisation
des barres trouées du jeu de construction Meccano est propice à la recherche
de configurations pour rigidifier les polygones. On
utilise des barres avec un nombre de trous quelconque et les boulons peuvent
être montés où l'on veut. La
fixation par boulon (vis plus écrou) n'est pas gage de rigidité de
l'assemblage. Il est nécessaire que la structure soit intrinsèquement rigide.
Meccano est un nom
déposé en 1907 par l’inventeur britannique Frank Hornby. |
Exemple de montage: une bissectrice
|
|
|
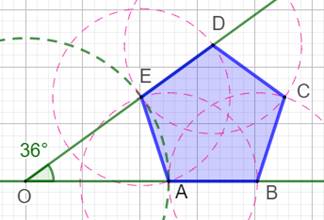
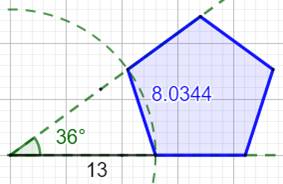
Pentagone Le
pentagone ABCDE est intercepté par l'angle DOB de 36°. Le triangle OAE est isocèle
(les angles en A et en E sont égaux). Notre défi: trouver des longueurs en nombres entiers (ou presque) pour OA et AE telles
que la construction avec des barres trouées de Meccano soit possible. Construction À partir d'un point O, construire un angle de
36°. Cercle de centre O et de rayon quelconque.
Intersections A et E. Des cercles de rayons AE (pointillés roses) déterminent
complètement le pentagone |
Note: le théorème de Laman assurant la rigidité s'applique
à condition de bien considérer que les segments OD et OB sont aussi des arêtes du graphe. Alors,
on a: P = 6 points et A = 9 arêtes et on a bien la relation de rigidité: 2P –
A = 3. |
|
|
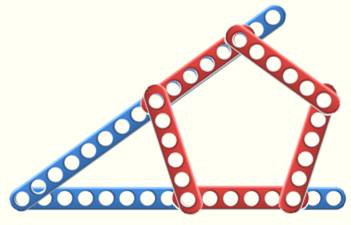
Idée Peut-on conserver ce montage en ayant des
longueurs proche d'une valeur entière pour
OA et pour AE ? Deux solutions avec OA inférieur à 20. Formule de calcul
Réalisation Meccano (8, 5) Note: les
longueurs sont suffisamment proches d'un entier pour permettre la
construction avec les barres trouées. |
Deux constructions possibles
|
|
|
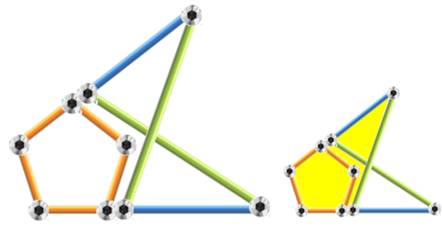
Autre idée Rigidifier le pentagone par deux barres vertes maintenant
deux côtés non adjacents prolongés (bleu). Avec une barre verte, on forme un quadrilatère
(jaune), donc non rigide. La seconde barre empêche la rotation de ce
quadrilatère. |
|
||
|
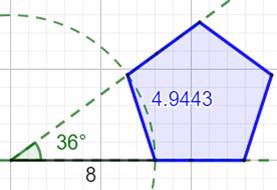
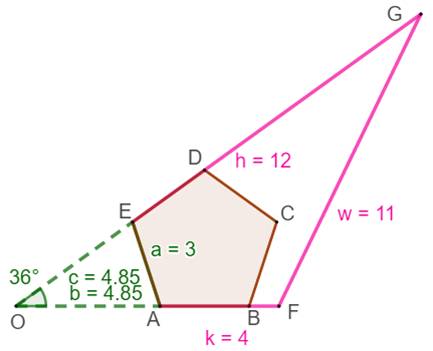
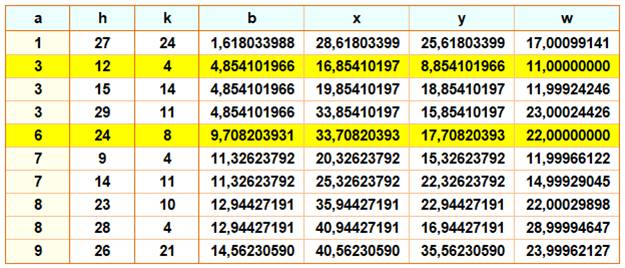
Longueurs des barres On souhaite que a, h, k et w soient des valeurs entières. Pour une valeur de a donné, on a: Voir Loi
des cosinus Une solution en valeur entière émerge pour a = 3, h = 12, k = 4 et w = 11 |
Pentagone "exactement"
rigide (valeurs entières)
|
||
|
Réalisation (3, 4, 12, 11) Le nombre
d'or se niche dans le pentagone.
Notamment:
Nombre entier exactement ! Le développement du calcul montre que:
Voir Puissance
de Phi |
Construction type Meccano
Côté du pentagone: 3 (pour 4
trous) Fixation sur barres bleues: 12
et 4 Longueur sur barres vertes: 11 |
||
Voir Brève de
maths n° 546
Deux
solutions en nombres entiers (en fait, la même)
et huit solutions approchées
Pour a jusqu'à 10
et (h, k) jusqu'à 30
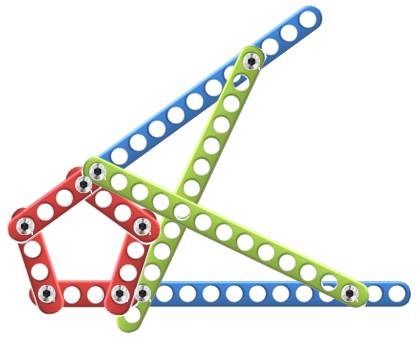
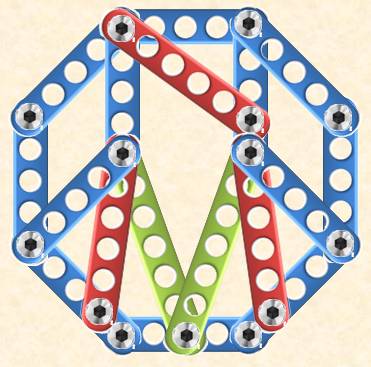
Exemples de montages avec le pentagone et l'octogone

![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/RigideM.htm
|