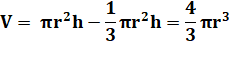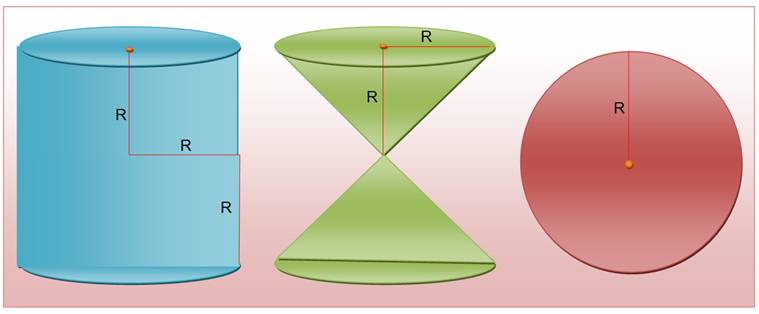
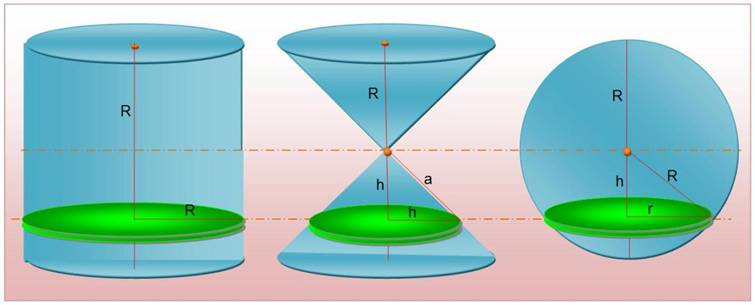
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/05/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	OBJETS 3D
Débutants Général	CÔNE, CALOTTE & CYLINDRE				Glossaire Géométrie
INDEX Géométrie	Cône	Sphère	Archimède	Ratio 123
		Cylindre
		Sommaire de cette page >>> Comparaison >>> Vu par Archimède >>> Sa méthode >>> Calculs

Comparaison entre ces trois volumes
Les trois volumes: cylindre, sablier et sphère Voir Cylindre / Cône / Sphère / Pyramide et tétraèdre – Comparaison Formulation des volumes Comparaison des trois volumes

Vu par Archimède

La sphère, ou plus exactement la boule, est équivalente en volume au "double-cône en creux", laissé libre lorsqu'on évide le cylindre par un double-cône. Vers 300 av. J-C., Euclide montre que le volume d'une sphère est proportionnel au cube de son diamètre. Il utilise la méthode d'exhaustion, en encadrant la sphère par des polyèdres. Proposition 18 du livre XII de ses Éléments. Vers 220 av. J.-C., Archimède a écrit dans De la sphère et du cylindre: Un cylindre qui a une base égale à un grand cercle d'une sphère, et une hauteur égale au diamètre de cette sphère, est égal à trois fois la moitié de cette sphère, et la surface de ce cylindre est aussi égale à trois fois la moitié de la surface de cette même sphère. Archimède est si fier de cette découverte qu'il donne des instructions pour que sa tombe soit gravée d'une sphère inscrite dans un cylindre. Voir Médaille Fields - Revers Cicéron (–106 à –43) a écrit Les Tusculanes. Il y indique avoir retrouvé la tombe d'Archimède marquée d'une sphère inscrite dans un cylindre. Plutarque (46–125) penseur et écrivain romain a écrit La vie des hommes illustres. Il y indique que l'inscription sur la tombe était une volonté d'Archimède. Anglais: The volume of a sphere is two-thirds the volume of its circumscribing cylinder.

Sa méthode
Archimède est le premier à calculer et prouver les formules de calcul de l'aire et du volume d'une sphère.	Il utilise la méthode d'exhaustion développée un siècle avant par Eudoxe de Cnide. Le calcul intégral sera inventé 1800 ans plus tard.
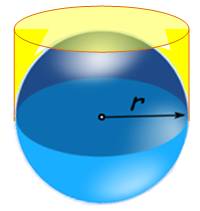
D'abord, il coupe la sphère en deux hémisphères pour disposer d'une section plane. Il enveloppe la demi-sphère d'un cylindre.
Ensuite, il la découpe l'ensemble en tranches (de saucisson ou de salami), toutes horizontales et aussi fines que possible.	Selon les tranches en partant du haut vers le bas, le diamètre reste constant pour le cylindre, alors qu'il croit pour la sphère. Ce dernier passe de Rt = 0 à Rt = Rcylindre.
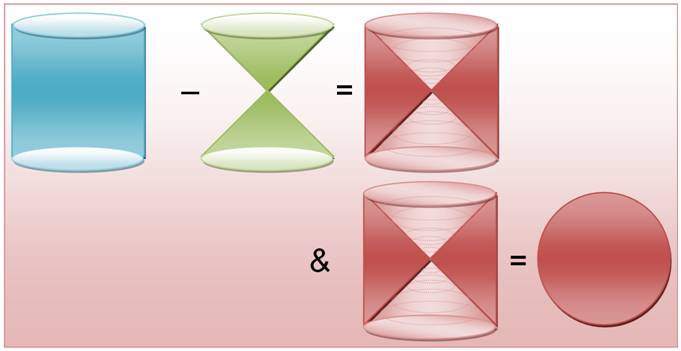
Archimède remarque que la différence entre les sections forme un cône dont la base est le cercle du cylindre	Vsphère = Vcylindre – Vcône
Deux volumes connus de lui, sachant que h = r

Calculs
Le principe utilisé par Archimède pour déterminer le volume de la sphère est équivalent à ceci: Chaque volume est découpé en fines tranches horizontales d'épaisseur e. Le rayon des tranches de cylindre reste constamment égal à R. Celui des tranches de cône (c) passe de R à 0 pour remonter vers R selon la distance h du centre du sablier au centre de la tranche. Le rayon des tranches de sphère (r) varie continument de 0 à R, puis de R à 0 selon la distance h du centre de la sphère au centre de la tranche. Il s'agit maintenant de comparer les volumes de chacune des tranches. Remarquons tout de suite que l'angle au centre du cône est un angle de 90° du fait que le cône a un rayon R et que sa hauteur est également égale à R. De sorte que le rayon de la tranche circulaire est égal à h.
Volume de la tranche du cylindre:
Volume de la tranche du sablier:
Volume de la tranche de la sphère:
Pythagore en action	R² = r² + h²
Conclusion:
La propriété est vraie pour chaque tranche; elle est vraie pour les volumes entiers. Les volumes décomposés en tranches restent encore formés de marches d'escalier. Mais, il est possible de passer à des tranches d'épaisseur aussi fine que l'on veut. Si bien qu'à la limite la propriété reste vraie pour les volumes parfaits.

Suite / Retour	Sphère Ratio 123 Calcul par tranches
Aussi	Archimède Cercle Cône Géométrie – Index Pyramides Pythagore Vocabulaire de la géométrie
DicoNombre	Nombre 0,666…
Sites	De la sphère et du cylindre (vers 225 av.J.-C.) par Archimède – Wikipédia Archimedes on Spheres and Cylinders – Math Pages The illustrated Method of Archimedes – Andre Koch Torres Assis and Ceno Pietro Magnaghi – pdf 49 pages
Cette page	http://villemin.gerard.free.fr/GeomLAV/Objet3D/CoArchim.htm