|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()

Voir Pensées & humour
|
Le problème de la chèvre dans un champ Revue de toutes les énigmes La chèvre
est dans un champ, Sans contrainte
particulière, la chèvre peut naturellement accéder à toute la surface
circulaire autour du pieu d'attache. Mais le champ peut être limité ou
encombré d'une grange ou … Selon le
type de contrainte, la solution du problème fait appel aux connaissances
allant de la géométrie élémentaire
jusqu'aux techniques d'intégration. |
|
|
||
|
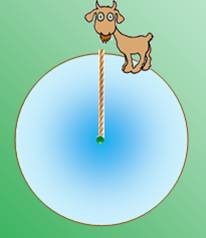
Chèvre
attachée simplement à son pieu avec une longe de 10 m. La
surface accessible est le disque de rayon 10 m dont l'aire est:
|
|
|
|
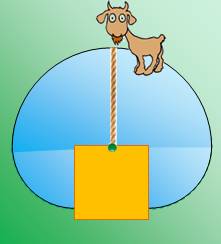
Cette
fois la longe est fixée sur le mur d'une grange de forme carrée. En général,
il s'agit d'un simple problème de géométrie abordable dès que l'on connait
l'aire du disque (CM2). Si la
longueur de la longe est telle que la chèvre peut aborder l'arrière de la
grange, le problème se complique car la chèvre peut aborder certaine zones en
passant d'un côté ou de l'autre. Il faut alors éliminer les surfaces qui
doublonnent. Le théorème
de Pythagore est appelé en renfort. |
|
|
|
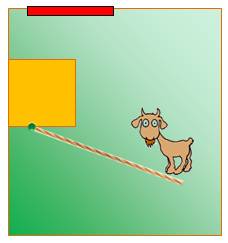
Una autre
type de problème demande à évaluer la longueur minimale d'une clôture (rouge)
à protéger pour éviter que la chèvre n'aille brouter dans le terrain du
voisin. |
|
|
|
L'imagination
peut conduire à poser la question pour toutes autre formes, notamment le triangle équilatéral. |
||
|
|
||
|
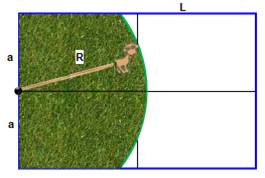
Le champ
est de forme rectangulaire
et la loge est attachée à un pieu situé au milieu de la largueur. Quelle la
longueur R de la corde pour que la chèvre soit en capacité de brouter
exactement la moitié du champ ? |
|
|
|
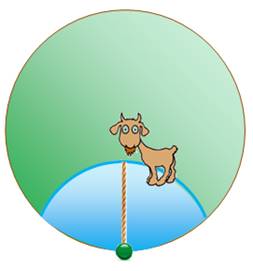
Le champ est
de forme circulaire et la longe est attachée à un point quelconque de
l'enclos. La chèvre
atteint une limite en forme de cercle tronqué. La surface accessible à la
chèvre est l'intersection de deux disques, surface appelée lentille.
Le calcul
de la surface est un problème de géométrie avancé, mais réalisable. Cependant, l'énigme
classique demande: quelle est la longueur de la corde pour que l'aire de
la zone bleue soit égale à l'aire restante de la zone verte? La mise en équation
n'est pas très simple mais réalisable. Par contre l'équation est insoluble
analytiquement. Seules possibilités: approximations successives (dichotomie) ou par
itérations (Newton)
ou encore calcul
intégral. |
Zone verte = Zone bleue pour
|
|
|
Dans cette
nouvelle situation, la longe est attachée à un silo à grain de forme cylindrique.
Lorsque
la chèvre explore le bas du champ, la
corde s'enroule autour du silo et sa longueur diminue progressivement.
L'extrémité balaie une sorte de spirale, en fait, une développante de cercle. La
résolution nécessite le calcul d'une intégrale. |
|
|
|
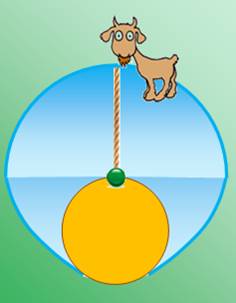
La chèvre
et la carotte. Sera-t-elle
capable d'atteindre la carotte ou le chou ou toute autre friandise? Il s'agit
de comparer la longueur de la longe à la distance entre la carotte et
l'anneau d'attache (point vert), situé en hauteur. |
|
|
Quelques autres énigmes mettant en
scène une chèvre sont indiquées dans l'en-tête.
|
|
|
|
Ce
problème est connu en anglais sous les noms suivants:
Longe,
corde ou laisse: tether Clôture:
fence Cabane, hangar, abri, étable: shed Enclos: paddock Pieu: pole A farmer owns a circular field of grass
(radius = r). He tethers a goat via a length of rope (R) to the circumference
of the field. What ratio r/R must the farmer choose so that the goat can only
eat half the area of grass? Given a circular field of grass of diameter
10 m. A farmer ties a goat to a pole on the circumference. When the rope is
taut, the goat path sweeps out an arc of a circle of radius R. The problem is
to determine the value of R so that the area of the ground accessible to the
goat is half of the circular field. |
|
Merci
à Jacques G. de Longueville pour sa contribution
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()