|
|||||||||||||||||||||||||||||
![]()
Un brin d'histoire
|
Le Français René Descartes (1596-1650) découvre seul la loi
qui porte son nom. En fait, avant lui, le Néerlandais Willebrord Snell l'avait formulée, mais sans la publier. Mieux! Cette loi était connue
bien avant par le mathématicien arabe Ibn Sahl
qui rédigea un traité en 984 sur les miroirs ardents et les lentilles. |
|
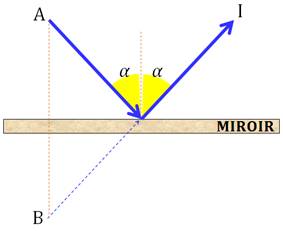
Réflexion Cas d'un rayon lumineux qui
se réfléchit sur un miroir ou d'une boule de billard qui rebondit sur la bordure.
Le rayon se réfléchit selon le même angle. La figure est symétrique. |
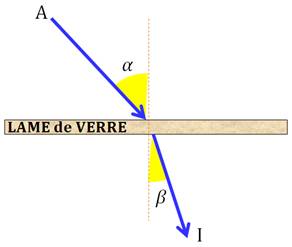
Réfraction Cas d'un rayon lumineux qui traverse une lame de verre ou qui pénètre
dans l'eau.
Le rayon traverse la lame de verre en formant un angle plus petit à la
sortie. |
Voir Principe
de Huygens / Diffusion et
diffraction
|
|
||||||||
|
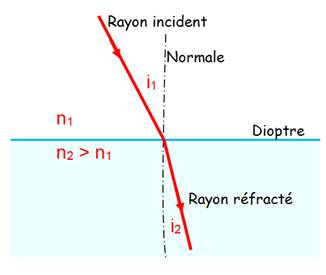
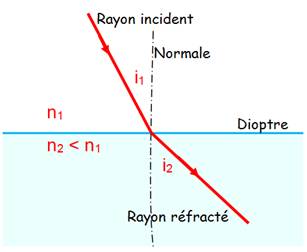
Loi de Snell-Descartes pour la réfraction.
Indices
Voici quelques indices:
|
||||||||
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
C'est ce qui se passe avec
le diamant. Ce phénomène explique son éclat. Mettez-le dans l'eau et ses feux
disparaissent.
sinus i lim = n2 / n1
Exemple
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Merci à Olivier Duwat
Une application: la taille des diamants
|
Taille peu profonde Deep cut |
Taille idéale Ideal cut |
Taille profonde Shallow cut |
|
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/OPTIQUE/LDSnell.htm |
![]()