NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/10/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	JEUX
Débutants Général	ALLUMETTES en CARRÉS						Glossaire Général
INDEX Allumettes Jeux et énigmes	Débutant	1 à 7 allumettes		BILAN	8 à 10	11 et 12		13 et 14
	Constructions	Jeux 1		Jeux 2	15 et 16	17 et 18		19 et 20
	Expert	Nombres		Quadrillage	Carrés Plan	Cube et 3D
			Sommaire de cette page >>> Rectangles >>> Combien de carrés? >>> Récapitulatif >>> Anglais

ALLUMETTES & CARRÉS

Ces pages sont consacrées aux jeux d'allumettes et, plus particulièrement, ceux consistant à dessiner des carrés. Outre les énigmes classiques, on y trouvera la liste des dessins possibles avec N allumettes et aussi le dénombrement de ces dessins lorsque cela est possible.

Cette page offre un petit divertissement pour commencer. La suite est un résumé récapitulatif des développements des nombreuses pages suivantes. Le sujet: avec k allumettes combien de carrés peut-on former?

Rectangles - Mise en bouche

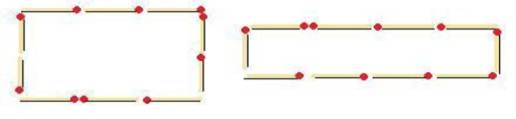
Cas simple Combien de rectangle peut-on former avec 10 allumettes? Deux seulement. Pourquoi pas plus? Les dix allumettes forment le périmètre du rectangle, lequel est égal à 2 (L + l). Conséquence: L + l = 5 et les deux seules partitions à deux termes de 5 sont 1+ 4 et 2 + 3. Avec 12, il y aurait trois possibilités car 6 = 1 + 5 = 2 + 4 = 3 + 3, le dernier étant un carré. Cas plus complexe Avec 60 allumettes? Avec 70? 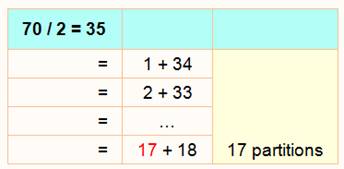Formulation générale On remarque que l'on divise K, la quantité d'allumettes, par 2 puis encore par 2 pour arriver au nombre de partitions (nombre en rouge), à un détail près, pour la seconde division par 2, on prend la partie entière. Soit la formulation générale pour au moins quatre allumettes: Retour sur les exemples 60 / 4 = 15 et 70 / 4 = 17,5 dont la partie entière est 17.

Voir Dénombrement

Combien de CARRÉS?
Ce dessin compte: 4 carrés de côté unité, et 1 carré de côté deux. Soit 5 carrés au total. Formé avec des allumettes, il faudrait 12 allumettes pour faire ce dessin. Avec une quantité d'allumettes donnée, combien de carrés peut-on former ?
On cherchera la quantité maximum de carrés de même taille: petits, moyens, grands, en relief … On notera quelques configurations panachées (pas toutes car très nombreuses…) Les pages suivantes illustrent les configurations indiquées dans le tableau récapitulatif ci-dessous.

Quantité de CARRÉS – Tableau récapitulatif

résentation	PLAN							3D
Côté	Max	< 1	1	2	3	4	5	Faces	Cubes

4 allu.	1	1
			1
5	2	2
6		3
	5	4	1
7	8	8
			2
8	14	13	1
		1	2
				1
9	20	20
		14	1
					3

10 allu.	30	29	1
		4	2
			3
			1	1
11	40	40
		8	3
		4			3
					4
12	55	54	1
		5	3
			4	1
					6	1
13	70	70
		7	3
			4
14	91	90	1
		11	3
			5
15	112	112
		13	3
			5	1
					6
16	140	139	1
		16	3
			5
17	168	168
		19	3
			6	2
18	204	203	1
		23	3
			6	1
19	240	240
		25	3
			6

20 allu.	285	284	1
		29	3
			5
			7	2
						11	2
21	330	330
22	385	384	1
			8	3
23	440	440
24	506	505	1
			9	4	1
25	572	572
26	650	649	1
27	728	728
			10	3	1
28	819	818	1
						16	3
29	910	910
			11	5	1

30	1015	1014	1
31	1120	1120
			12	6	2
32	1240	1239	1
33	1360	1360
						20	4
34	1496	1495	1
			13	7	2
35	1632	1632
36	1785	1784	1
			14	7	2
37	1938	1938
38	2109	2108	1
			15	8	3
39	2280	2280

40	2470	2469	1
			16	9	4	1
41	2660	2660
							25	5
42	2870	2869	1
43	3080	3080
			17	10	4	1
44	3311	3310	1
45	3542	3542
			18	10	4	1
46	3795	3794	1
46							29	6
47	4048	4048
			19	11	5	1
48	4324	4323	1
49	4600	4600
			20	12	6	2

Note: Non exhaustif au-delà de 50

50	4900	4899	1
51	5200	5200
							33	7
52	5525	5524	1
52			21	12	6	2
53	5850	5850
54			22	13	6	2
54							36	9
56			23	14	7	2
58			24	15	8	3

60

25

16

9

4

1

Présentation	PLAN							3D
Côté	Max	< 1	1	2	3	4	5	Faces	Cubes

Les pages suivantes (telles qu'indiquées dans l'en-tête de cette page),

illustrent toutes les configurations indiquées ci-dessus >>>

English corner

Matchstick puzzles or stick puzzles Puzzle or pastime with matches or toothpicks or sticks of wood. A number of matchsticks are arranged as squares, rectangles, triangles or any kind of drawing. The challenge consists in rearranging the matches so that a new drawing is created Generally a given number of matches are to be moved or removed. Sometimes these puzzles are not just about making geometric shapes. They do need some cunning tricks calling for specific (lateral) thinking. They were popular when, to light on candles or oil lamps, almost everyone carried a box of matches with them.

Suivante	Carrés avec 1 à 7 allumettes
Voir	Jeux avec des allumettes Chiffres romains Carrés Dénombrement – Index Tables de valeurs – Index Diconombre – Index
Sites	Puzzle Playground - Matchstick Puzzles Age of Puzzles - Matchstick Puzzles Les allumettes de Pierre Berloquin
Cette page	http://villemin.gerard.free.fr/aJeux1/Allumett/Allume01.htm