|
||||||||||||
Transformations usuelles
|
Sens commun:
|
Avant transformation Après transformation
Les transformations
multiples du papillon (Aussi, au sens courant: la chenille
devient chrysalide et se transforme en papillon) |
|
|
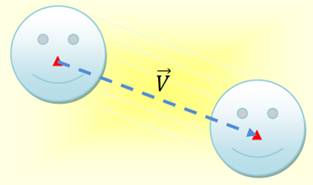
Deux glissades: une courte et une plus
grande
La figurine a été translatée selon la flèche en bleu Translation de vecteur |
Suite en Translation
|
|
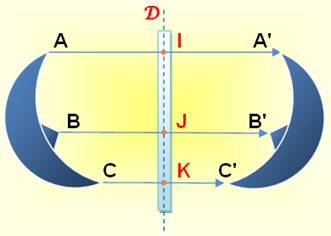
Queue – Corps – Tête |miroir| Tête –
Corps – Queue
Chaque point d'un couple est à égale
distance du miroir Symétrie par rapport à une
droite |
Suite en Symétries
|
|
En six heures, la petite aiguille
effectue une rotation
d'un demi-tour
Rotation par rapport à un
point |
Suite en Rotation
|
En tout ca, tout le dessin est transformé
dans la même proportion.
|
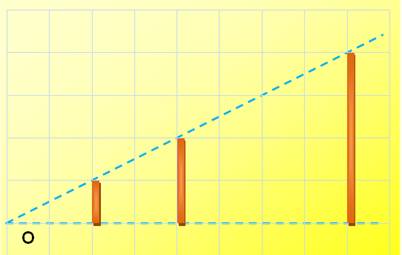
Bouquet de ballons plus ou moins gonflés
Taille ½ Taille 1 Taille 2 Homothéties de centre 0 et de rapports ½ et 2 |
Suite en Homothétie
Propriétés des transformations
|
Ce mot vient du grec: iso (pareil, égal) métrie (mesure). |
Ces deux figures sont
isométriques Le
rectangle reste rectangle Le
triangle reste un triangle Le
cercle reste un cercle Le
cœur reste un cœur Les
parallèles restent des parallèles Les
angles droits restent des angles droits Les
longueurs sont conservées |
Suite en Isométrie
|
On aurait pu prendre le cas des plaques
d'immatriculation des voitures: une voiture possède son numéro et pour un
numéro il y a une voiture et une seule.
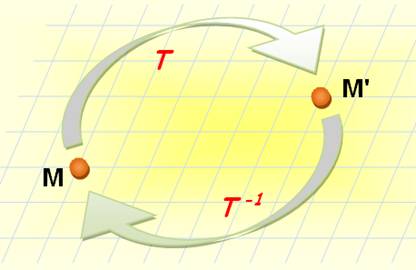
Exemple: la
rotation d'origine O et d'angle 30°; sa transformation réciproque est la
rotation de même origine et d'angle -30° (rotation du même angle, mais en
sens inverse; en marche arrière). |
Chaque personne a un numéro de sécurité sociale. À chaque numéro de sécurité
sociale correspond une personne.
Tout point M' a
un seul antécédent: un point M Tout point M a une seule image: un point
M' La transformation f est
bijective Toutes les transformations vues ci-dessus
sont bijectives. |
Suite en Bijection
|
Pourquoi tout cela ? Remarquez que, finalement, nous avons
trois "objets": le dessin d'origine, le dessin-image et la
transformation. Si nous connaissons les propriétés de deux d'entre eux, nous
connaissons automatiquement les propriétés du troisième. Par exemple, la
transformation est une rotation; trois points sur le dessin d'origine sont
alignés; eh bien, sur l'image, ils seront aussi alignés. |
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()