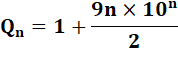NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/11/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	BASES de l'arithmétique
Débutants Nombres	ADDITIONS			Glossaire Nombres
INDEX CALCUL	Addition	Somme des chiffres	Somme de 1 à 100
		Sommaire de cette page >>> Additions dans la table d'additions >>> SOMME des NOMBRES de 0 à 10 – Triangles >>> SOMME des NOMBRES de 0 à 9 – Deux à deux >>> SOMME des CHIFFRES des nombres de 0 à 99 >>> SOMME des CHIFFRES des nombres de 0 à 1 000 000

ADDITION - SOMME

Jouons avec la somme des nombres successifs

et la somme de leurs chiffres.

Commençons avec une propriété surprenante des tables d'additions.

Rappel de vocabulaire

Addition = opération >>>

Somme = résultat de l'addition

Chiffres = symboles de 0 à 9 >>>

Nombres = suites de symboles pour exprimer une quantité >>>

Voir DicoMot Math

Additions dans la table d'additions

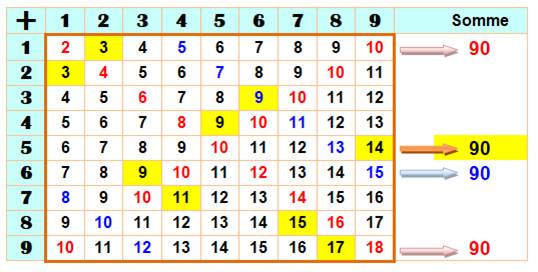
Soit la table d'addition des nombres de 1 à 9. Sur chaque ligne, prenez un nombre dans une colonne différente. Le résultat d'un tel choix se nomme une permutation figurée, typiquement rencontrée dans les carrés latins. La somme de ces neufs nombres est toujours 90. À droite, on montre quatre exemples: les deux diagonales avec nombres en rouge, une pseudo- diagonale qui commence par 5 en nombres bleus, et une permutation figurée (lignes et colonnes au hasard) en jaune. Explication Aucun mystère ! Chaque nombre du tableau est l'addition de deux nombres: celui de la ligne et ce sont les nombres de 1 à 9; celui de la colonne et, du fait de la logique de construction de la permutation, on y retrouve une fois chacun des nombres de 1 à 9. 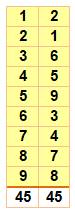Chaque somme partielle (1 + 2 + … + 9 = 45) contribue à la somme totale: 2 × 45 = 90. 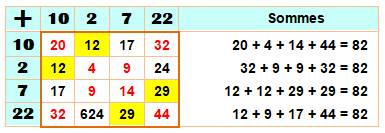Illustration avec les sommes de l'exemple avec une permutation figurée (jaune) Somme magique Elle vaut 2 (1 + 2 + … + n) = 2n (n + 1) / 2 = n (n + 1) Ce sont les nombres oblongs ou proniques: 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, … Généralisation Cette propriété est valable pour toute sous-grille carrée extraire de la table d'addition et cela dans n'importe ordre: Exemple Note: les nombres à ajouter peuvent être différents sur la ligne et sur la colonne.

Voir Brève 48-940 / Multiplications dans la table de multiplications / Tour de magie

SOMME des NOMBRES de 0 à 10

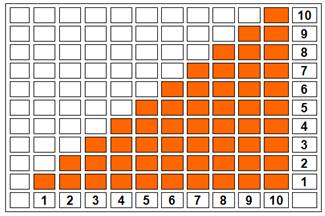
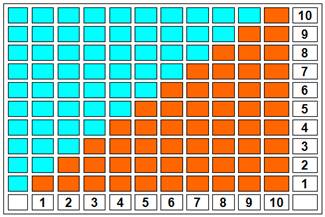
La solution en images

La somme 1 + 2 + 3 … + 10 peut se représenter par une sorte de triangle fait de piles de briques de hauteur égale aux nombres successifs, jusqu'à 10.

Posons le même triangle inversé par dessus.

Le triangle rouge contient 1 + 2 + 3 … + 10 briques. Le triangle bleu également. Le rectangle contient 2 fois cette somme.

Avec les deux triangles nous formons un rectangle de 10 de haut et de 10 + 1 de longueur. Nous connaissons l'aire de ce rectangle: 10 x 11 = 110. Et l'aire d'un des triangles: 110 / 2 = 55

La somme des nombres de 1 à 10 est donc simplement 55. Et, la formule générale:

Somme des nombres de 1 à n: S = n (n + 1) / 2

Exemples

Nombres de 1 à	Leur somme
10 20 30 40 50 60 70 80 90 100	55 210 465 820 1 275 1 830 2 485 3 240 4 095 5 050

SOMME des NOMBRES 0 à 9
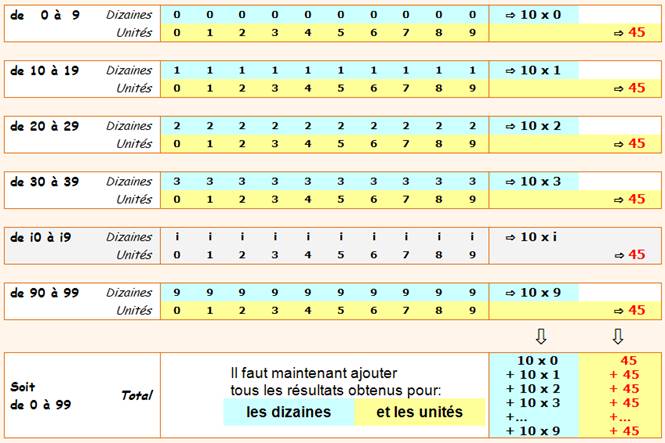
Voici la méthode qu'utilisa Gauss enfant pour faire une telle somme: regrouper les nombres deux par deux. Somme des chiffres de 0 à 9 ou somme des nombres de 0 à 9 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 Somme des chiffres des nombres de 0 à 10 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 1 + 0 = 46

SOMME des CHIFFRES des nombres de 0 à 99

Nous savons que la somme des nombres est égale à 1 + 2 + 3 + … + 99 = 99 x 100 / 2 = 4 950. Mais quelle est la somme des chiffres de ces nombres? On procéde par tranche de dizaines successives: on retrouve notre somme des nombres de 0 à 9; et les sommes des chiffres des dizaines. Nous disposons des sommes partielles par dizaines. Effectuons les totaux. les dizaines 10 x 1 + 10 x 2 + 10 x 3 + … + 10 x 9 = 10 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 10 x 45 = 450 et les unités 45 + 45 + 45 + … + 45 = 10 x 45 = 450 Soit en additionnant les deux résultats: 450 + 450 = 900. Somme des chiffres des nombres de 0 à 99 = 900 Somme des chiffres des nombres de 0 à 100 = 901

Voir Nombre 901

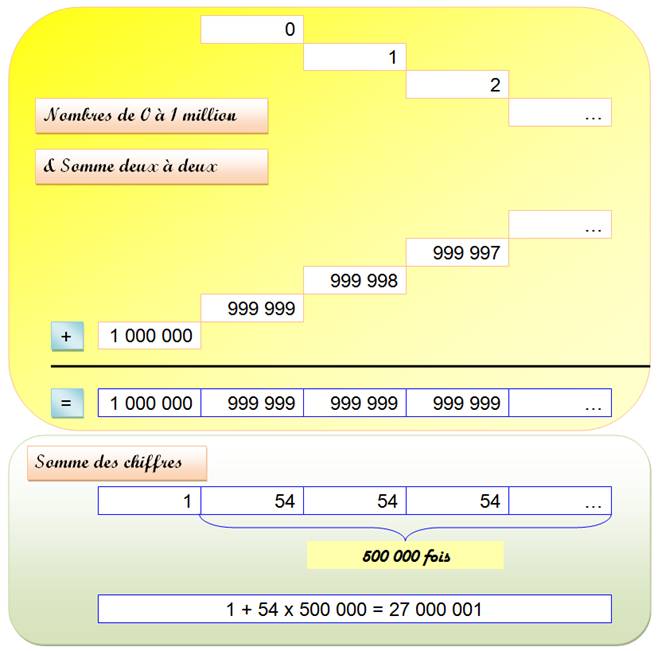
Somme des chiffres des nombres de 0 à 1 million
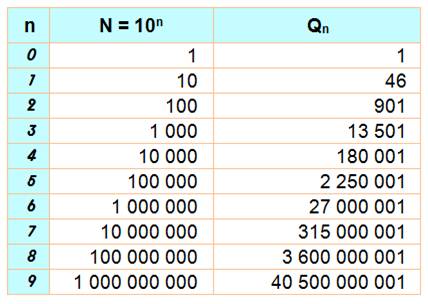
En disposant les nombres en colonne de deux comme indiqué, la somme est très facile à exécuter. Formalisation Somme des chiffres jusqu'à N = 10^n Valeurs

Voir Somme des chiffres des nombres

BILAN

Somme des nombres de 0 à 9 Somme des chiffres des nombres de 0 à 9 Somme des chiffres des nombres de 0 à 10 Somme des nombres de 0 à 10 Somme des chiffres des nombres de 0 à 99

45 45 46 55 900

Suite	Soustraction
Voir	Barre magiques des premiers Calcul mental Carrés Magiques Débutants Édouard Lucas Euros et divisions par 3 Fractions Gauss Jeux Multiplication Nombres triangulaires Pascaline Plus et moins dans les multiplications Preuve par neuf Progression Arithmétique Quantité de segments dans un polygone Sommes des entiers, carrés … Théorie des nombres
DicoNombre	Nombre 10 Nombre 900 Nombre 1 million
Cette page	http://villemin.gerard.free.fr/Calcul/Operatio/AddiSomm.htm