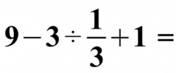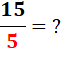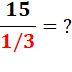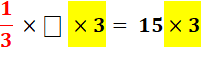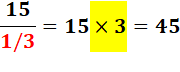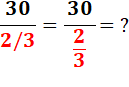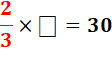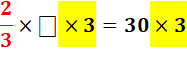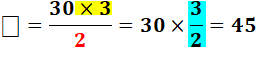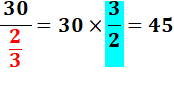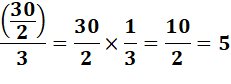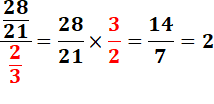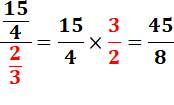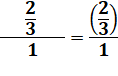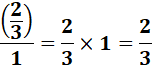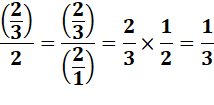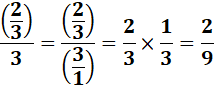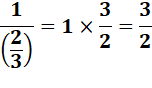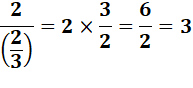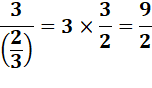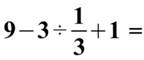|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Fractions – DIVISION La division
simple n'est pas simple! Mais une fois le truc compris, elle devient plus
facile. Pour la division des fractions, bonne nouvelle! C'est le même truc! Pour diviser 6 par 2, je me pose la question:
combien de fois 2 font 6? Ou encore, il y a combien de 2 dans 6? Pour diviser 6 par 1/2, je me pose la question:
combien de demis dans 6. Je visualise les parts de tarte si nécessaire. J'en
vois 12.
Les six galettes de la ligne du haut deviennent douze demi-galettes lorsque coupées en moitiés. |
Voir Cours de 5e sur
les fractions
|
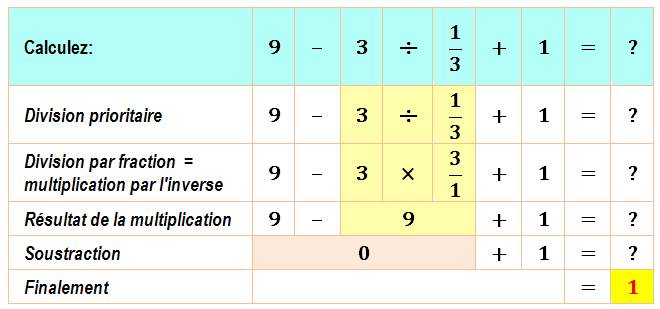
Calculez
Calculez
cette expression qui fait le tour d'Internet en 2016.
|
|
|
||
|
Division des nombres entiers Le concept de division n'est
pas facile à acquérir. Comment être sûr de cette
connaissance et de sa pratique quasi-automatique avant de sauter le pas et
aborder la division des fractions? La division est une
multiplication à trous. Quel est le facteur
manquant? |
La division vue de différentes manières
Combien de 5 dans 15 ? 5 fois combien font 15 ?
Quel est le nombre à mettre dans le carré pour satisfaire
cette égalité? |
|
Tiers
|
Combien
y a-t-il de tiers dans 15? Je
visualise 15 galettes divisées en trois et je compte 45 morceaux. |
|
|
||
|
Division des fractions Appliquons la recherche du
facteur manquant. |
|
|
|
Bon d'accord, mais je ne
suis pas plus avancé! Que dois-je faire? |
Le truc, ici, c'est d'appliquer
une propriété des égalités: On ne change
rien à une égalité si tous
les facteurs sont multipliés par le même nombre. |
|
|
Ici, nous allons tenter de
nous débarrasser du dénominateur en multipliant par 3 |
|
|
|
Le but est atteint nous
avons "supprimé" la fraction en ayant créé un produit égal à 1. |
|
|
|
Résultat en pratique Je remarque qu'il suffit de
multiplier par l'inverse de la fraction: 1/3 devient 3/1 = 3. |
|
|
Demis et quarts
|
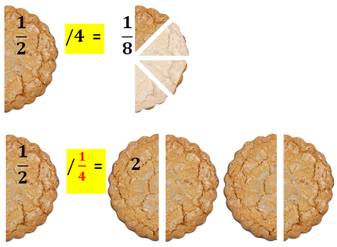
Combien
y a-t-il de quarts dans un demi? Combien
ça fait ½ divisé par ¼ ? Pas
facile! Voyons en images comparatives.
|
|
|
||
|
Cette fois le numérateur est
différent de 1. |
|
|
|
Cela revient à la
multiplication à trous |
|
|
|
Comme précédemment, je
supprime la fraction du dessous en multipliant par 3 |
|
|
|
Calcul en simplifiant par 3 |
|
|
|
Deux fois ce que je cherche vaut
30 x 2; alors pour une seule fois, je divise par 2. |
|
|
|
Je remarque que diviser par
une fraction, c'est multiplier par la fraction inverse (retournée) |
|
|
|
Remarque: attention à la place des traits de fraction.
Trente demis divisé par 3 égal 15, puis divisé par 3 donne bien 5. |
|
|
|
|
||
|
Cette fois le numérateur est
différent de 1. La manière de faire reste la
même. |
|
|
|
Le plus souvent, le résultat
est une fraction. |
|
|
Voir Fractions à
étages
|
|
||
|
Surprenant à première vue,
mais respectons notre règle. Attention à ne pas calculer
trop vite. Note: lorsque
le graphisme le permet, on peut montrer les fractions avec des traits plus
grands:
|
|
|
|
Ne pas confondre avec la
division d'un entier par une fraction. Avec l'unité au numérateur
la fraction se retrouve inversée. C'est même la définition de l'inverse. |
|
|
|
Première
question
Seconde
question
|
Retour / Autres devinettes qui affolent le
Net
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()