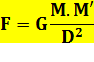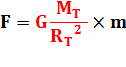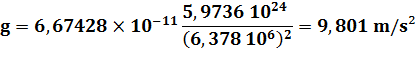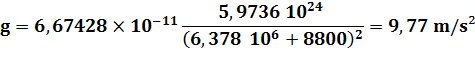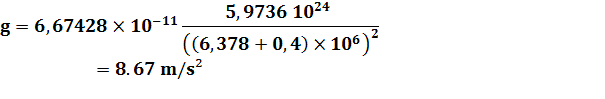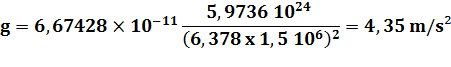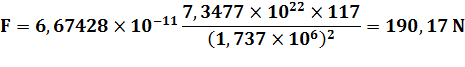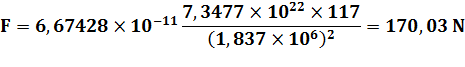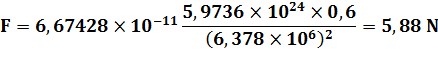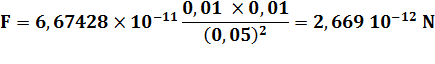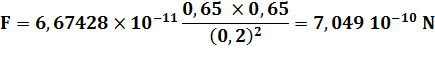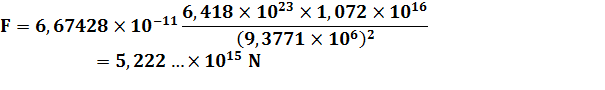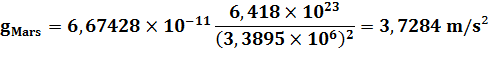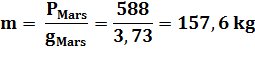NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/05/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Physique
Débutants Général	CHUTE LIBRE				Glossaire Général
INDEX Gravitation SCIENCES	Gravité	Pesanteur	Chute	Calculs
	Seconde	Sommaire de cette page >>> Gravitation et pesanteur – Rappels >>> Station orbitale ISS – Principe de calcul >>> Gravité terrestre – Pesanteur >>> Astre de rayon double de celui la Terre >>> Poids sur la Lune >>> Ballon sur la Terre >>> Deux billes >>> Boules de pétanque >>> Phobos et Mars >>> Homme sur Mars – Masse apparente >>> Homme en ascenseur

Gravitation et pesanteur

Quelques exemples de calculs. Niveau physique de la classe de seconde.

Gravitation et pesanteur – Rappels
Gravitation universelle (s'applique aux objets qui gravitent) G est la constante de gravitation universelle	pour M et M' en kilogrammes D en mètres F en newtons
Pesanteur (s'applique aux objets pesants) Simple application de la gravitation au cas de la Terre. g est l'accélération de la pesanteur
Un objet de masse 100 kg est attiré par la Terre avec une force pèse En langage courant	F = 981 N P = 981 N P = 100 kgf (kilogramme-force)
Pour vérifier les ordres de grandeurs, on peut mentalement convertir les newtons en kgf.	En gros, 10 fois moins de "kilos" que de newtons

Station orbitale ISS Principes de calcul – Repère
Altitude Tour de la Terre Masse		400 km 92 min 50s = 5 570 s 450 tonnes = 4,5 10^5 kg
Référentiel	Géocentrique Le référentiel Géocentrique est un solide constitué par le centre de la Terre et des étoiles lointaines dont les positions n’ont pas varié depuis des siècles. Le référentiel géocentrique est un référentiel Galiléen (dans lequel s'applique le principe de l'inertie).
Mouvement	Circulaire uniforme. Le principe de l'inertie n'est pas vérifié. Principe de l'inertie: sans actions extérieures, un objet reste: soit au repos, soit en mouvement rectiligne uniforme. La station orbitale est soumise à des forces qui ne se compensent pas. La station est soumise à l'attraction universelle de la Terre.
Rayon de la Terre Rayon de l'orbite Longueur de l'orbite		6 378 km 6 338 + 400 = 6 738 km L = 2 x 6 738 = 42 336,10 km
Vitesse de la station		v = L / T = 42 336,10 / 5 400 = 7, 8400 … km / s
Force d'attraction par la Terre		F = m . g = 4,5 x 10^5 x 8,67 = 3,901 10^6 N

Gravité terrestre (pesanteur)
Rayon de la Terre Masse de la Terre	R = 6 378 km = 6, 378 10^6 m M = 5,9736 10^24 kg
Valeur de g à la surface (altitude 0) Valeur de g à une altitude de 8 800 m (Himalaya) Valeur de g à une altitude de 400 km (Station orbitale ISS) Valeur de g à une altitude de R/2 = 3 189 km soit à une distance 1,5 R du centre de la Terre Voir Tracas de calcul avec les puissances

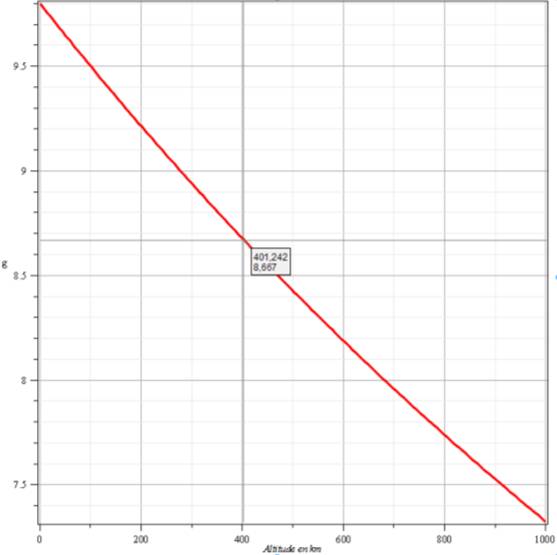
Valeur de g selon l'altitude: de 0 à 1000 km

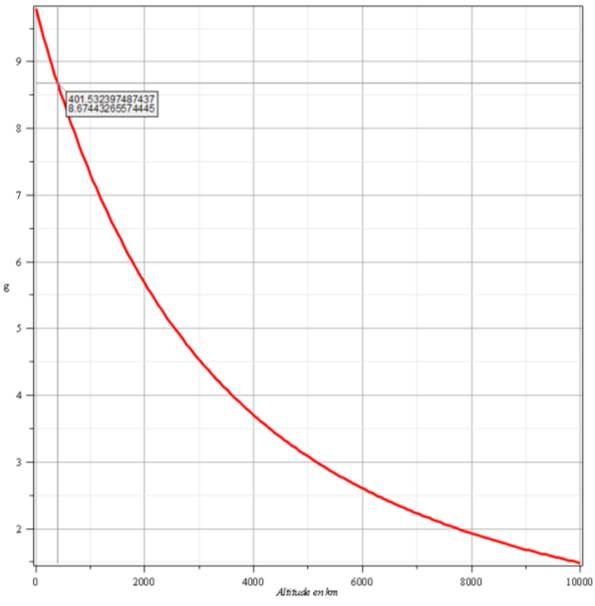
Valeur de g selon l'altitude: de 0 à 10 000 km

Astre de rayon double de celui de la Terre
Rayon de l'astre	RA = 2RT
Masse de l'astre de même densité que la terre Rapport des volumes comme le cube des rayons Masse de l'astre	MA = VA x d MT = VT x d MA / MT = VA / VT VA / VT = (RA / RT)^3 = 2^3 MA = MT x 2^3
Gravité de l'astre Gravité de la Terre Rapport	gA = G x MA / RA² gT = G x MT / RT² gA / gT = MA / MT x RT² / RA² = 2^3 / 2^2 = 2

Poids sur la Lune
Masse de la Lune Rayon de la Lune Masse de l'objet sur Terre	7,3477 10^22 kg 1 737,4 km 117 kg
Poids de l'objet sur la Lune:
Poids de l'objet dans une capsule spatiale à 100 km d'altitude:

Ballon sur la Terre
Rayon de la Terre Masse de la Terre Masse du ballon	R = 6 378 km M = 5,9736 10^24 kg m = 0,6 kg
Force exercée par la Terre sur le ballon et réciproquement:

Deux billes
Masse de chaque bille Distance entre boules	10 g = 0,01 kg 5 cm = 0,05 m
Force exercée par une boule sur l'autre:

Boules de pétanque
Masse de chaque boule Distance entre boules	0,650 kg 0,20 m
Poids d'une boule	0,65 x 9,81 = 6,3765 N
Force exercée par une boule sur l'autre:

Satellite Phobos de la planète Mars
Masse de Mars Masse de Phobos Rayon orbital de Phobos	M = 6,418 10^23 kg m = 1,072 10^16 kg R = 9 377,1 km
Force exercée par Mars sur Phobos et réciproquement:

Un homme sur Mars
Masse de Mars Rayon de Mars Masse d'un homme	M = 6,418 10^23 kg R = 3 389,5 km = 3, 3895 10^6 m m = 60 kg
Force exercée par Mars sur l'homme: Poids de l'homme sur Mars et comparaison (Rapport: 2, 63) L'homme a la sensation de "peser" seulement: 223,8 / 9,81 = 22,8 kg. À l'inverse, si un homme pèse 588 N sur Mars, c'est que sa masse est:

Un homme en ascenseur
Un homme dans un ascenseur est en train de se peser. L'ascenseur monte avec une accélération de 3 m/s². Quel est le poids ressenti par l'homme, indiqué sur le pèse-personne?
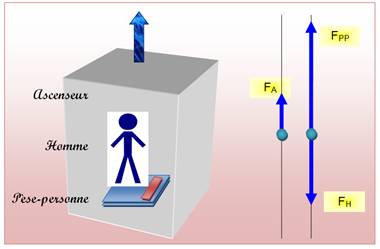
Force de soutien du pèse-personne Poids de la personne Force agissant sur l'ensemble		FPP FH = m . g FA = m . a = FH + FPP
Force de soutien du pèse-personne		FPP = FA – FH = m . a – m . g = m (a – g) = 75 (3 – (–9,81)) = 75 x 12,81 = 960,75 N
Masse apparente dans l'ascenseur		960,75 / 9,81 = 97,93 kgf
Avec l'ascenseur qui descend avec la même accélération Masse apparent à la descente		FPP = 75 (– 3 – (–9,81)) = 75 x 6,81 = 510,75 510,75 / 9,81 = 52,06 kgf

Voir La commande logique d'un ascenseur – Diaporama Junior

Suite	Pesanteur Chute libre au centre de la Terre
Voir	Physique – Index Vitesse – Glossaire
Aussi	Dicomot
Cette page	http://villemin.gerard.free.fr/aScience/Physique/Chute.htm