|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
FRACTIONS MYSTÈRES
|
|
|
||
|
Formalisons cette égalité. Même dénominateur Identité remarquable
a² – b² Simplification qui montre
que: avec a + b = d, nous obtenons la fameuse
égalité des fractions. |
a² – b² = (a – b) d (a + b) (a – b) = (a –
b) d a + b = d |
|
|
|
||
|
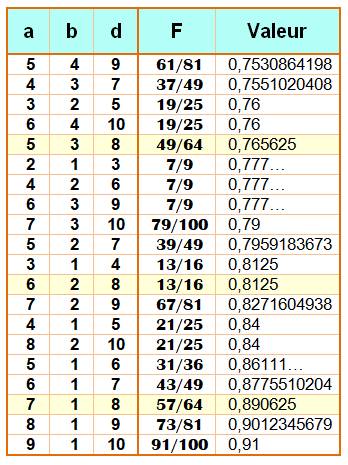
Toutes les égalités jusqu’à d
= 10, ordonnées selon la valeur croissance des fractions. En jaune, les égalités avec
d = 8 vues ci-dessus. |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()