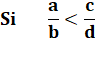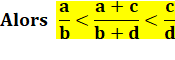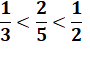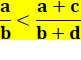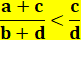|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
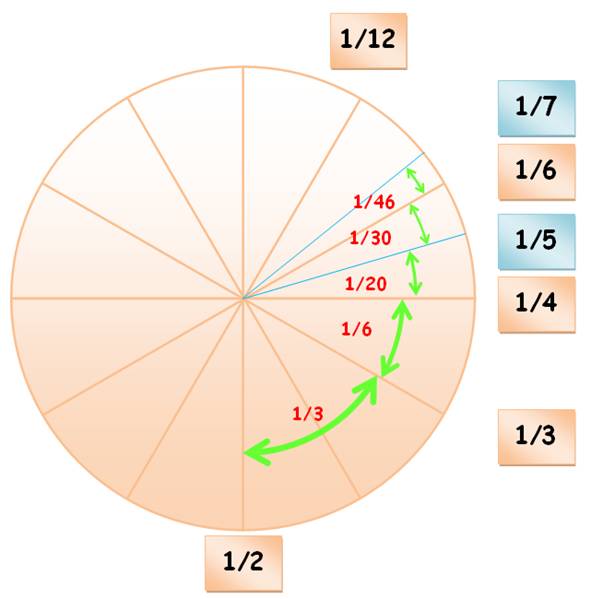
FRACTIONS USUELLES Comparaison entre les fractions en
dixièmes (celles de tous les jours, du décimètre …) et celles en douzièmes
(celles de l'horloge). En passant une propriété de
comparaison entre fractions. |
|
|
||
|
Défi Trouver une fraction dont le
numérateur est inférieur à son dénominateur et telle qu’elle soit égale à une
fraction dont le numérateur est plus grand que le dénominateur. |
Réponse Il faut recourir aux nombres
négatifs. Par exemple :
Le nombre - 2 est plus petit que 3,
et le nombre 2 est plus grand que –3. |
|
|
|
|
|
Exemple
Table 1/ a = 1/ b
+ 1/ c 1/a = 1/b + 1/c 1/ 2 1/ 3 1/ 6 0,50000 0,33333 0,16667 1/ 3 1/ 4 1/ 12 0,33333 0,25000 0,08333 1/ 4 1/ 5 1/ 20 0,25000 0,20000 0,05000 1/ 5 1/ 6 1/ 30 0,20000 0,16667 0,03333 1/ 6 1/ 7 1/ 42 0,16667 0,14286 0,02381 1/ 7 1/ 8 1/ 56 0,14286 0,12500 0,01786 1/ 8 1/ 9 1/ 72 0,12500 0,11111 0,01389 1/ 9 1/ 10 1/ 90 0,11111 0,10000 0,01111 1/ 10 1/ 11 1/ 110 0,10000 0,09091 0,00909 1/ 11 1/ 12 1/ 132 0,09091 0,08333 0,00758 1/ 12 1/ 13 1/ 156 0,08333 0,07692 0,00641 1/ 13 1/ 14 1/ 182 0,07692 0,07143 0,00549 1/ 14 1/ 15 1/ 210 0,07143 0,06667 0,00476 1/ 15 1/ 16 1/ 240 0,06667 0,06250 0,00417 |
|
Voir Suite
du tableau
Voir Fractions
demi, tiers … / Maths de
l'horloge / Horloge
|
Fractions
dont le dénominateur est égal au numérateur moins un. Ce
sont des nombres exceptionnels: additionnés ou multipliés au numérateur, ils
donnent le même résultat.
|
|
|
||
|
Question Si la
fraction a/b est inférieure à la fraction c/d montrez cette inégalité. Réponse On
suppose que ces nombres sont positifs différents de 0, notamment pour éviter
que les dénominateurs soient nuls. La fraction
obtenue est appelée fraction médiane. Voir Convergence
Fibonacci-Nombre d'or |
Inégalité (propriété)
Exemple
En effet: 0,333… < 0,4 < 0,5 |
|
|
Première inégalité en
produit croisés: Ajoutons ab (positif): Factorisation: Décroisement du produit: |
|
|
|
Même procédure, en joutant
cd. |
|
|
|
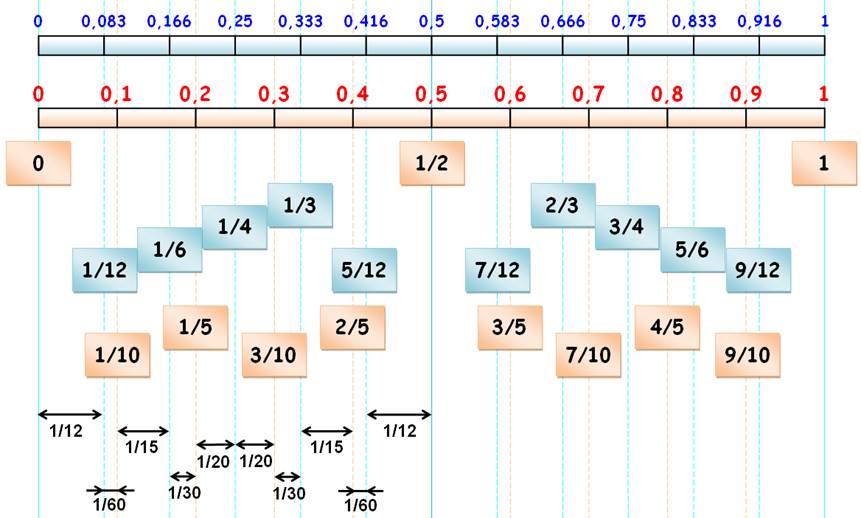
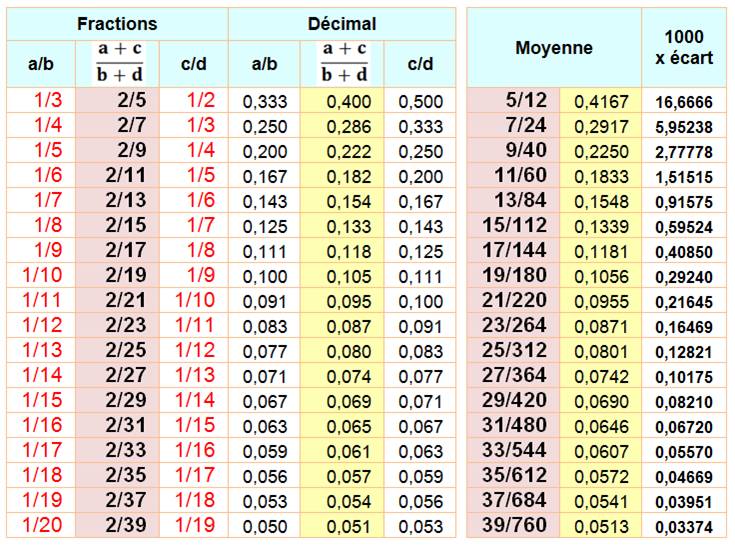
Exemples en tableau On compare les fractions:
a/b = 1/n et c/d = 1/(n+1). Exemple de lecture: pour 1/3 et 1/2,
la fraction intermédiaire est 2/5 qui vaut 0,4 en décimal. À comparer à la
moyenne entre ces deux fractions qui vaut 5/12 = 0,416; un écart avec la
fraction intermédiaire de 16,6 /1000.
|
||
Voir Application à un tour de magie /
Fractions illicites / Brève
571
![]()
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Cette page |
![]()