NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/05/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	LOGIQUE
Débutants Logique	Autour du raisonnement				Glossaire Logique
Index des pages Logique >>> INDEX >>> Rubriques	Dualité		Raisonnement	Incomplétude
	Logique de Boole		Logique formelle	Logique floue
	Dichotomie		Trichotomie
		Sommaire de cette page >>> Dichotomie >>> Exemple >>> Dichotomie variable – Irrégularité de distribution >>> Toutes les factions en 1/k avec k de 2 à 17

Dichotomie
Raisonnement par dichotomie: procédé de recherche qui consiste à déterminer si l'objet de la recherche est dans la première moitié ou la seconde. La moitié concernée est exploitée de la même manière: l'objet recherché est dans la la première moitié ou la seconde. Ainsi de suite.

Exemple
Elle vient d'acheter une paire de chaussures à 72 euroset décide de faire deviner le prix à son mari. Chéri, cette paire de chaussure vaut moins de 100 euros, saurais-tu en deviner le pris exact? Plus de 50 euros. Oui. Plus de 75 euros; Non … Voir illustration

Dichotomie variable – Irrégularité de distribution
Phénomène curieux en cherchant à placer des nombres dans des intervalles de fractions progressives. Le problème numérique Il s'agit donc de trouver une série de nombres dans l'intervalle tels que: Les deux premiers appartiennent à chacune des moitiés; Les trois premiers, à chacun des tiers; Les k premiers à chacune des portions en 1/k.	Résultat Le résultat surprenant est que cela est possible mais jusqu'à k = 17 seulement. Impossible pour 18. Historique Découverte due au polonais Hugo Steinhaus (1887-1972). Démontré par Berlekamp et Graham en 1970

Anglais: Irregularity of distributions

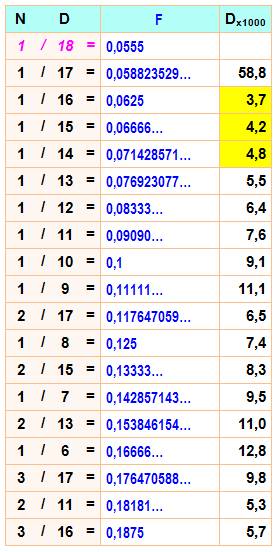
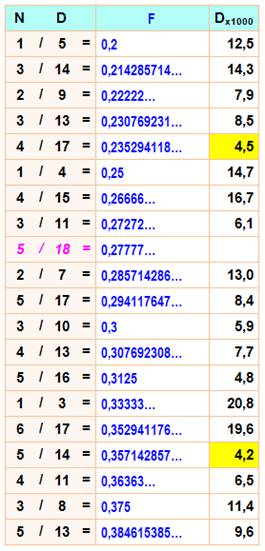
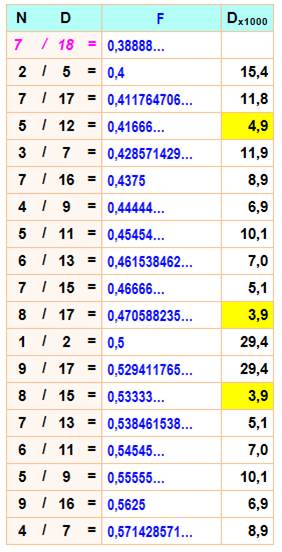
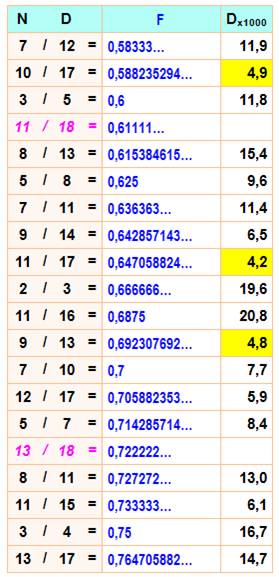
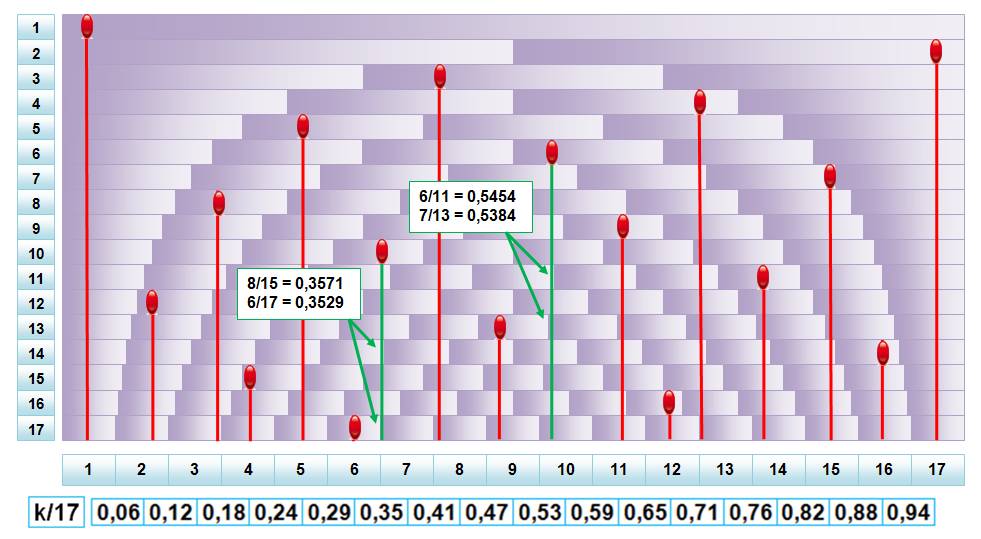
Illustration: une des possibilités de placement de 17 nombres

17 traits dont 2 verts qui montrent la place restreinte pour ces deux là.

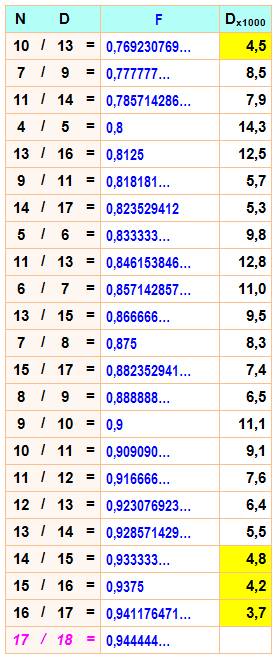
Toutes les factions en 1/k avec k de 2 à 17 plus celle en 1/18 en rose

La colonne D_x1000 donne l'écart entre les valeurs successives en millièmes.

En jaune les zones étroites à moins de 5/1000.

Voir Fractions – Index / Tables – Index / Développement décimal des fractions

Merci à Axel S. pour l'idée de cette page

Suite	Dualité Binaire Parité Résolution équation du quatrième degré
Voir	Calculs avec les pairs et impairs Deux et culture Outils de la logique Raisonnement
Sites	Irregularity of distributions – Wikipedia Irregularities in the distributions of finite sequences – E.R. Berlekamp et R.L. Graham
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Logique/Dichotom.htm