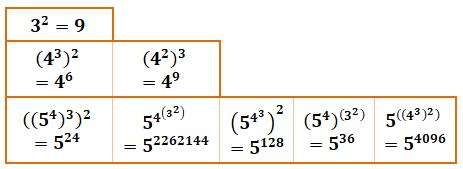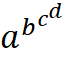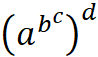|
Édition du: 29/03/2023 |
|
INDEX |
Dénombrements - MOTIFS |
|||||
|
Nombres de
Catalan – Développements |
||||||
Faites
un double-clic pour un retour en haut de
page
![]()
|
NOMBRES DE CATALAN Parenthèses, arbres,
exposants Combien de façons de disposer les parenthèses. Analogies avec les graphes. |
||
|
|
Sommaire de cette page >>>
Paires de parenthèses bien ordonnées >>>
Programmation Maple pour parenthèses >>>
Parenthèses & Arbres >>>
Avec cinq nombres >>>
Exemple de l'hexagone >>>
Arbres et exposants |
Débutants Glossaire |
Anglais : Catalan Numbers
|
Paires de parenthèses bien ordonnées ou parenthèses bien équilibrées ou
mots bien parenthésés |
|
|
La quantité de n paires de parenthèses bien
ordonnées (une parenthèse ouvrante trouvera sa parenthèse fermante) est égale
au nombre de Catalan de rang n. Exemple Cas n = 3: ( ( ( ) ) ), ( ( ) ) ( ) , ( ( ) (
) ) , ( ) ( ( ) ), ( ) (
) ( ) Code:
111000
110010 110100 101100 101010 Le code vaut 1 pour une parenthèse ouvrante et 0 pour la fermante. Le
code comporte autant que 1 que de 0. Pour chaque chiffre, la quantité de 0 à
gauche est inférieure ou égale à la quantité de 1 à gauche. Voir Mots de Dyck TABLE pour n de 1 à 7
>>> |
|
|
Programmation Maple
pour parenthèses bien ordonnées Le programme est récursif (il
fait appel à lui-même). Deux pointeurs sont mis en place:
|
||
|
|
But Énumérer toutes paires de parenthèses valides
(motifs) pour n donné. Commentaire La procédure Su
fait passer d'un cas au suivant en gérant les pointeurs e et f et créant les
motifs. Trois paramètres: E, F et P P est le code binaire représentant les
parenthèses. Un test initial qui, si e et f sont nuls,
autorise l'impression du motif. Un test 1, tant que e n'est pas nul, crée une
parenthèse ouvrante et crée le besoin d'un fermante (e = e – 1 et f = f + 1). Le test 2 est déclenché si f est positif, cad.
s'il y a un besoin de créer une parenthèse fermée. En bleu, le résultat du traitement pour n= 3. Notes de
programmation Maple n'admet pas qu'on
calcule sur la paramètres d'entrée: d’où passage (E, F, P) à (e, f, p). L'appel à la procédure se
fait avec les paramètres mis à jour dans l'instruction. Ne pas les préparer à
l'avance. |
|
|
Chemins de traitement pour n = 2
|
Pour suivre le parcours récursif du
programme c1, c2 indiquent le chemin pris. Les deux chiffres suivants sont les valeurs de e
et f qui indiquent le compte des parenthèses ouvrantes et fermantes. Le nombre binaire de droite est la configuration
en cours de formation. Le nombre à gauche est la configuration finale
proposée. Notez que si le chemin 1
est exécuté, alors que le chemin 2 devait l'être aussi, dans ce cas le
programme met les paramètres de côté pour les reprendre plus tard, une fois
qu'il aura complètement traité le chemin 1 et ses suites (principe de la
récursivité). |
|
|
Listing du programme pour
copier-coller dans Maple restart; Su := proc (E,
F, P) local e, f, p; e := E; f := F; p := P; if e = 0 and f = 0 then
lprint(p); return end if; if 0 < e
then Su(e-1, f+1, 10*p+1) end if; if 0 < f then Su(e, f-1, 10*p) end if
end proc; n := 3: Su(n, 0, 0): |
||
Voir Programmation – Index / Programmation
avec Python (et autres)
Parenthèses binaires
|
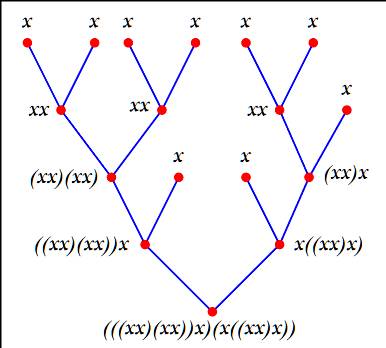
Paire de parenthèse sur un mot de n + 1 lettres Pour n = 3: (xx٠x)x, x(xx٠x), (x٠xx)x, x(x٠xx), xx٠xx Représentation par un arbre Montre comment le mot final (en bas) peut être créé à partir d'un
arbre dont les feuilles sont x.
Source images: Stanley |
Anglais: Binary parenthesis of a string of n+1 letters
|
Compter les parenthèses On considère n + 1 lettres (considérées comme des
variables dans une expression algébrique). Deux lettres, au moins, sont entre parenthèses. Combien de possibilités? Codage Le code est produit de la façon suivante:
Pour quatre lettres, par exemple, le code
comprend quatre "0" et trois "1" pour trois jeux de
parenthèses. |
|
|||||||||||||||||||||||||||||||||||||||||||
|
Les 14 motifs avec au moins une paire de
parenthèses enfouies contenant deux nombres. |
|
|
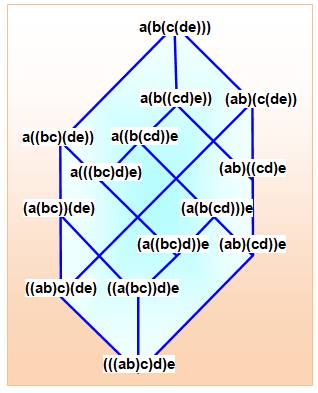
Avec 5 lettres Treillis de Tamari d'ordre 4 Les 14 mots avec parenthèses. Un treillis de Tamari est un ensemble partiellement ordonné dont les
éléments sont les différentes façons de grouper une suite d'objets en paires
avec parenthèses. Par exemple, pour la suite abcd de quatre objets,
il y a cinq groupements possibles, qui sont : ((ab)c)d, (ab)(cd), (a(bc))d,
a((bc)d), et a(b(cd)). Les mots avec parenthèses sont appelés: produits non associatifs. Produit du fait de la
présence de lettres représentant des facteurs, et non associatif car la place
des parenthèses importent. On note que ces produits sont aussi
non-commutatifs; les lettres (facteurs) ne peuvent pas être permutées. |
|
|
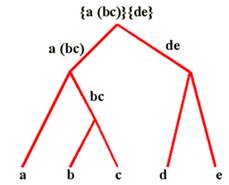
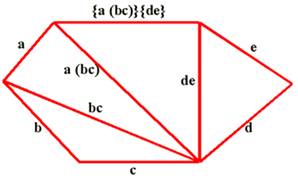
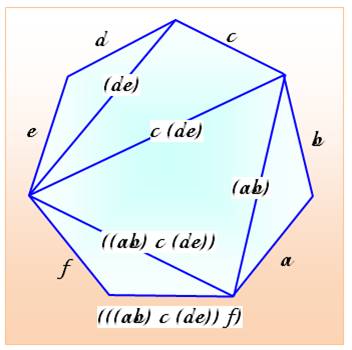
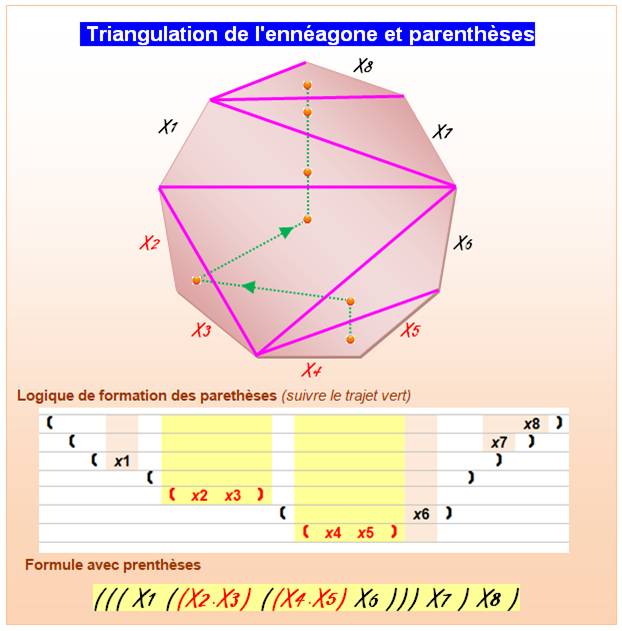
Hexagone: un exemple On peut représenter une mise en parenthèses par
un graphe ou par un polygone découpé. Il existe 14 = C4
motifs. |
|
|
Heptagone: un exemple Il existe 42 = C5
motifs. |
|
Voir Nombres de Narayana
|
Arbres Cinq configurations avec 3 flèches et leurs correspondances en positon des exposants. Voir
Arbres-Catalan |
Les cinq motifs en arbres
|
|||||||||||||||||||||||||||||||||||
|
|
De n = 1 à 3
Les cinq motifs en puissances Formules en écriture classique (puissances à étages) et
écriture linéaire ou ordinateur.
Valeurs (exemple) Les colonnes reprennent les expressions des colonnes correspondantes
vues ci-dessus.
Lecture (( 2^2)^2)^2 = 256 ou
(( 2^3)^2)^3 = 262 144 |
|||||||||||||||||||||||||||||||||||
Anglais: Laddered exponents
![]()
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPDENOM/Catalan/CataExpo.htm
|
|
![]()