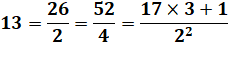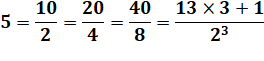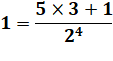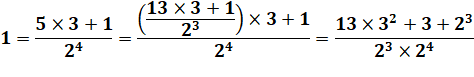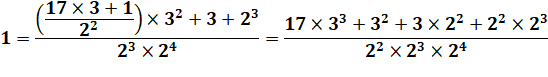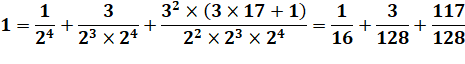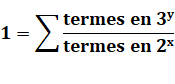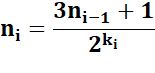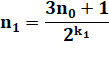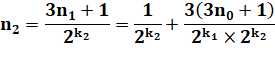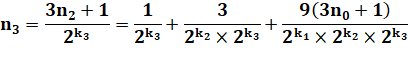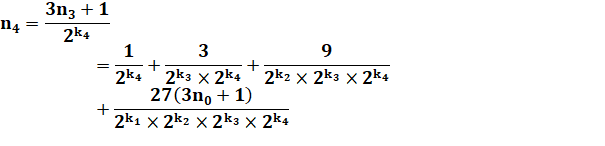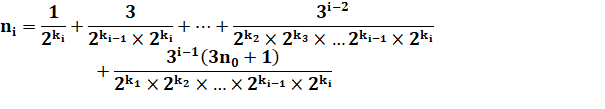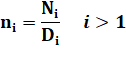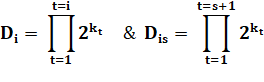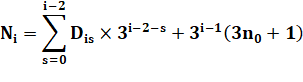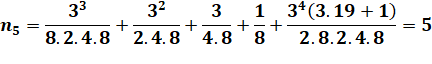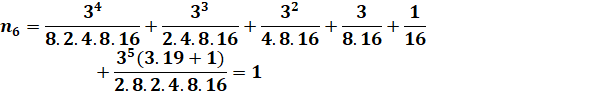|
|||||||||||||||||||||||||||||||||||
|
Syracuse et Algèbre Cycle impossible? Sommes en 2x & 3y
Outre le
cycle autour du 1, un autre cycle court est impossible. Une
manière originale de voir la suite de Syracuse de chaque nombre (suite de
Collatz) consiste à l'exprimer sous forme symbolique. Une voie vers la
démonstration de la conjecture ? |
Voir Programmation
Syracuse – Débutant (Tableur et
programmation)
|
|
|||
|
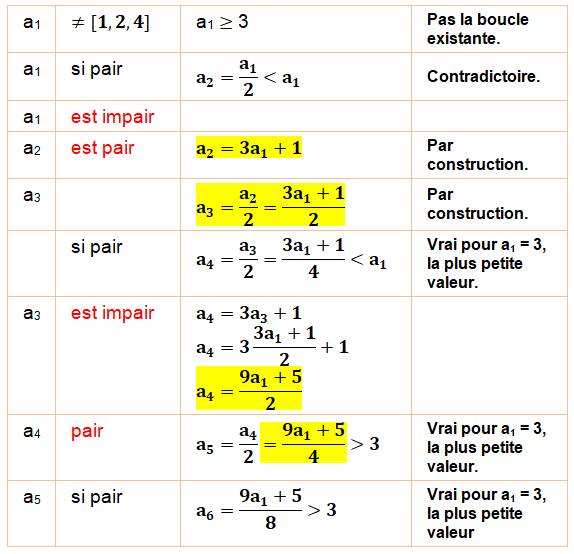
Supposons un cycle dont le plus petit nombre est a1. Ce
nombre ne fait pas partie du cycle connu [1, 4, 2, 1…]. Le tableau montre les déductions possibles sur la parité et sur la
valeur des nombres successifs. Aucun ne peut égaler a1. Donc, pas
de cycle avec ces cinq nombres. Que a5 soit pair ou impair, a6 est de toute
manière encore plus grand que a1. Conclusion: aucune boucle possible avec 2 à 6 nombres. |
|
||
|
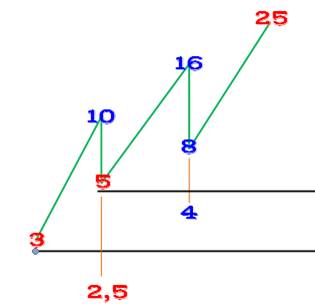
Ce petit graphique peut aider à suivre le raisonnement exposé
ci-dessus dans le cas critique où a0 = 3. Impossibilité de
rejoindre le 3 initial. Même phénomène avec le 5. On s'éloigne encore plus du nombre initial avec des nombres plus
grands (6, 7, 8 …). |
|
||
|
|
||||
|
Cycle de Collatz pour n impair Nous nous
intéressons aux nombres impairs et notons l'arrivée du nombre impair suivant
(en rouge). On passe
du 17 au 13 en trois étapes, autant que l'exposant du 2 au dénominateur plus
un. On peut
résumer de la manière suivante: 172,
133, 54, 1 Les
indices indiquent la quantité de division par 2 entre deux impairs. |
Exemple 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
|
|||
|
Calcul complet Tentons
la remontée complète: |
|
|||
|
Observations D'abord
émerveillons-nous de cette somme de trois fractions égale à 1. Ensuite,
voyons la structure: des puissances de 2 au dénominateur et de 3 au
numérateur. |
Somme des trois fractions
Structure de la somme
|
|||
Voir Puissances de 2
/ Puissances
de 3
|
|
|||
|
Valeur
d'un nombre impair en fonction du précédent:
|
|
||
|
En partant du premier nombre n0. |
|
||
|
Il me semble plus facile d'exprimer la formule
concise en mettant l'ensemble au même dénominateur:
La conjecture de Syracuse indique que ni finit par valoir
1; que la somme de toutes ces fractions vaut 1. Cette formule met bien en évidence les puissances
de 2 et de 3. Par contre, elle est d'un usage limité car les
valeurs de k ne sont pas connues a priori. |
|||
|
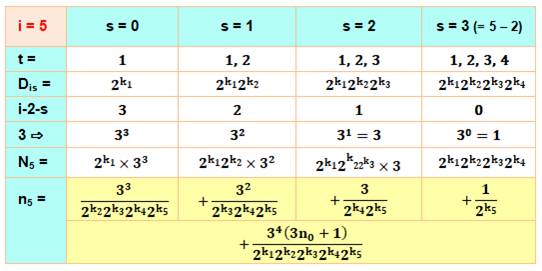
Exemple de développement de la formule pour n5
Exemple avec 19 (21 étapes) 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5,
16, 8, 4, 2, 1 => 192, 298, 112, 174,
138, 516 Les indices 2, 4, 2, 4, 8, 16 représentent k1, k2
.. k6.
|
|||
|
Nous avons mis au point une
formulation algébrique de la conjecture de Syracuse. Est-il possible d'en
faire quelque chose? D'en déduire l'inéluctable occurrence d'une somme
égale à 1 ? Pas si simple …. Pour poursuivre la réflexion: |
|
Voyez le document de Wilfrid Poulain
qui propose une étude en généralisant la suite:
avec en dénominateur la plus grande
puissance de 2 divisant le numérateur. Voir sa page Suite impaire symbolique de Collatz étendue à kn + 1 20 août 2017 |
|
Voyez également l'article de 2011 du prodigieux mathématicien Terence Tao: The
Collatz conjecture, Littlewood-Offord
theory, and powers of 2 and 3 et
l'énorme forum de discussion qui suit. |
Je remercie Wilfrid Poulain pour
l'idée de cette page
|
Retour |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Iteration/Syracus3.htm
|
