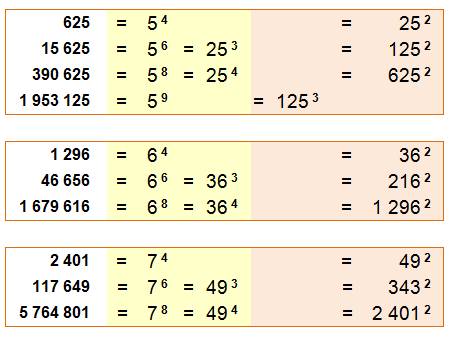NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/12/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	NOMBRES
Débutants Nombres et Puissances de 10	PUISSANCES			Glossaire Puissances
INDEX Puissance Décomposition	Calculs	Multi-puissances	Exposants	Consécutives
	Nombres puissants (2-P, 3-P)		Nombre ABA (AB^A)	Apocalyptique
	Nombres n^k · k = …kkk…
		Sommaire de cette page >>> Passage d'une puissance à une autre >>> Exemple >>> Cas de puissances cachées >>> Table

NOMBRES MULTI-PUISSANCES

Nombre égal à la puissance d'au moins deux nombres.

16 = 2⁴ = 4²

Passage d'une puissance à une autre
Si les deux puissances a^n et b^m sont égales, alors quelles sont les relations entre a et b d'une part, et m et n d'autre part? En divisant l'exposant par k, on élève le nombre à la puissance k.

Illustration par un exemple
P2 = élévation à la puissance 2; D2 = division par 2. Règle Une puissance peut s'exprimer sous toutes les formes correspondant à un diviseur de l'exposant. Ici: diviseurs de 18 = {1, 2, 3, 6, 9, 18}, soit six formes.

Cas de puissances cachées
Comment interpréter: 32^3 = 8^5? Les exposants ne sont pas divisibles ! En fait, un exposant se cache dans 32, car: 32 = 2^5. Le premier nombre s'écrit alors: 32^3 = (2^5)^3 = 2^5x3 = 2^3x5 = (2^3)^5 = 8^5 Illustration La règle énoncée ci-dessus s'applique à condition de faire ressortir les puissances cachées. Ici 32^3 = 2^15 et les diviseurs de 15 sont: {1, 3, 5, 15}.

Table jusqu'à 1 million
Puissances de 2 Puissances de 3

Puissances de 5, 6 et 7

Puissances de 8 (en fait puissances de 2)

Table développée pour exemple de puissances cachées

Autre puissances de 8 jusqu'à un million

Assez banales, puisqu'il s'agit du couple carré et bicarré.

Suite	Exposants à étages Puissances et chiffres permutés Puissances – Table de valeurs
Voir	Puissance – Index Puissances de 2 Puissances de 2 à 5
Cette page	http://villemin.gerard.free.fr/aNombre/PUISSANC/PuisMult.htm