|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Les 21 problèmes NP-complets de Karp Domaine de la théorie de la complexité
des algorithmes. Sujets: combinatoire,
graphes Contributeur Richard Karp (né en 1935) en 1972.
Prix Turing en 1985. Le regroupement par thèmes est mon
propre choix. |
Voir Problème du voyageur
de commerce et problème P = NP
|
|
||
|
PARTITION |
Problème
de partition:
il s'agit de partager exactement (partitionner) un ensemble de nombres entiers
en deux sous-ensembles
tels que la somme des nombres de l'un soit égale à la somme des nombres de
l'autre. Exemple: {1, 2, 2, 3, 3, 4, 5} => {1, 2,
3, 4} et {2, 3, 5}. |
|
|
SET COVERING EXACT COVER |
On
dispose de sous-ensembles. Avec eux, il s'agit de retrouver tous les éléments
d'un autre ensemble en utilisant une quantité minimale de ces sous ensembles. Exemple: {1,2}, {3,5},{1,2,3},{4,5,6,7}
pour{1,2,3,4,5,6} Une
couverture exacte est celle réalisées avec des sous-ensembles disjoints
(aucun éléments communs). Exemple: {1,2}, {3,5},{3,4},{4,5,6}
pour{1,2,3,4} |
|
|
HITTING SET |
Le
problème de l'ensemble intersectant consiste à trouver un sous-ensemble
contenant au moins un élément de chacun des ensembles d'une famille. De
plus, la quantité d'éléments est limitée. |
|
|
3-DIMENSIONAL MATCHING
|
Appariement
à 3 dimensions: on dispose de trois ensembles disjoints (X, Y, Z) et d'un jeu
de contraintes. Le problème consiste à décider s'il existe un ensemble (U) de
triplets associant un élément de chaque ensemble (X, Y, Z) sous contrainte
avec une quantité minimale d'éléments. Exemple: comment associer des hommes, des
femmes et des chats en triplets homme-femme-chat avec des contraintes de
compatibilité (certains n'aiment pas les chats ou les gros nez …) |
|
|
|
||||
|
SATISFIABILITY |
Problème
SAT: problème de décision, qui, étant donné une formule de logique
(avec des Et, Ou, Non …), détermine s'il existe une valeur des variables qui
rend la formule vraie.
La
réponse est "vrai" ou "faux" sans se soucier de la valeur
des variables. |
|||
|
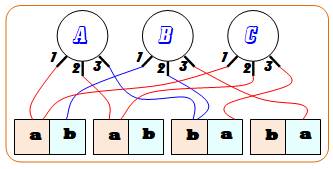
3-SAT |
Forme
particulière du problème SAT avec trois variables par clause logique.
Illustration
naïve Les carrés de la
figure sont nommés a ou b au choix. Les ronds ont trois bras. Chacun doit être
relié à un carré a ou b au moins. Un problème 3-SAT se pose la question:
est-il possible de nommer les carrés de sorte que chaque rond soir relié à un
carré de type a, au moins? Résolution évidente ici.
|
|||
|
|
||
|
CHROMATIC NUMBER |
La
coloration
de graphe consiste à attribuer une couleur à chacun de ses sommets de
manière que deux sommets reliés par une arête soient de couleur différente. Le
nombre minimal de couleurs est appelé nombre
chromatique. |
|
|
VERTEX COVER |
Le
problème de couverture par sommets consiste, étant donné un graphe,
à trouver un ensemble minimum de sommets pour couvrir toutes les arêtes. |
|
|
CLIQUE CLIQUE COVER |
Problème
de la clique: problème algorithmique qui consiste à trouver des cliques dans
un graphe. Clique:
sous-ensemble de sommets d'un graphe tous adjacents les uns aux autres,
également appelés sous-graphe
complet. Le
problème de la couverture par cliques est le problème algorithmique
qui consiste à trouver une couverture par cliques minimale. |
|
|
FEEDBACK ARC SET FEEDBACK NODE SET |
Préoccupation
qui consiste à supprimer des arcs du
graphe pour éliminer des circuits indésirables. Préoccupation
qui consiste à supprimer des nœuds du
graphe pour éliminer des circuits indésirables. |
|
|
DIRECTED HAMILTONIAN
CIRCUIT UNDIRECTED HAMILTONIAN
CIRCUIT |
Un
chemin
hamiltonien est un chemin qui passe par tous les sommets
une fois et une seule. Rappel:
un graphe
eulérien est un chemin qui passe par toutes les arêtes
une fois et une seule |
|
|
MAX-CUT |
Problème
de la coupe maximum: comment partitionner un graphe en deux graphes complémentaires
de sorte que la quantité d'arcs soit maximale dans les deux sous-graphes. |
|
|
|
||
|
STEINER TREE |
Un
arbre relie tous les points d'un réseau. Si la longueur totale est minimale,
il s'agit d'un arbre
de Steiner. |
|
|
KNAPSACK |
Problème
du sac à dos: problème d'optimisation
du contenu d'un sac à dos. Comment obtenir un poids minimum et une valeur
maximale avec des objets de poids et de valeurs connus. Voir Optimisation linéaire. |
|
|
SET PACKING Empaquetage d'ensemble |
Problème
d'un sac à dos multidimensionnel où les poids des objets sont égaux à 0 ou 1
et où les capacités du sac sont toutes égales à 1. |
|
|
0-1 INTEGER
PROGRAMMING |
Optimisation linéaire (ou
programmation linéaire) ne faisant intervenir que des nombres entiers pour la
fonction de coût comme pour les contraintes. Similitude
avec équations
diophantiennes |
|
|
JOB SEQUENCING |
Séquençage
de tâches ou planification: sous contraintes de durée, de coûts, de
ressources, etc. Comment
ordonnancer les tâches ? Des
pénalités sont infligées en cas de dépassement. Quelle est la séquence des
tâches qui minimalise les pénalités ? |
|
Voir Énigmes de
rythme de travail
|
Suite |
|
|
|
Voir |
||
|
DicoNombre |
|
|
|
Sites |
|
|
|
Cette page |
||
![]()