Logique et modèles à raisonnement

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/08/2020 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	LOGIQUE
Débutants Logique	Domaines				Glossaire Logique
INDEX Logique	Dualité	Logique de Boole	Logique formelle		Logique floue
	Raisonnement	Intelligence	Démonstration		Incomplétude
	Historique	Logique des propositions		Théorie des ensembles
		Sommaire de cette page >>> Tout sur les logiques >>> Énigme & paradoxe >>> Paradoxe >>> Ontologie >>> Syllogisme >>> Sorite >>> Déduction & induction >>> Fourchette de Hume

Un jour j'irai vivre en Théorie parce qu'en Théorie tout va bien.

Toute vérité franchit trois étapes. D'abord, elle est ridiculisée. Ensuite, elle subit une forte opposition, puis elle est considérée comme ayant toujours été une évidence.

Schopenhauer

Des affirmations extraordinaires réclament des preuves plus qu'ordinaires. Carl Sagan

Quod gratis asseritur, gratis negatur.

Ce qui est affirmé sans preuve peut être rejeté sans preuve.

Formule du droit Romain, aujourd'hui appelé rasoir d'Hitchens (1949-2001).

Voir Pensées & humour

RAISONNEMENT

LES ARCANES DE LA LOGIQUE

Sujet peu abordé car difficile. En fait, déroutant par ses paradoxes. Il n'existe pas beaucoup de méthodes ou de moyens simples pour traiter et résoudre les énoncés de logique de raisonnement. Essayez donc de décortiquer cette phrase: "Je suis un menteur".

Voir Paradoxe du menteur

Tout sur les LOGIQUES
RAISONNEMENT	LOGIQUE MATHÉMATIQUE	ÉNIGMES
DÉDUCTION	LOGIQUE FORMELLE	PARADOXES
AUTO – RÉFÉRENCES	INTELLIGENCE ARTIFICIELLE	ABSURDE
Démonstrations (preuve)	Automatisation	Induction

Voir Logique – Index / Test du QI

Types de raisonnement

Inductif, déductif, par récurrence, par dichotomie, par contraposition.

Fausse position

ÉNIGME & PARADOXE

Une énigme a une solution ou une hypothèse qui évite une contradiction.

Dans un paradoxe, aucune des hypothèses n’est valable.

PARADOXE

Séries de prémisses raisonnables dont on déduit une conclusion qui contredit les prémisses.

Le faux raisonnement:

Erreur bien dissimulée dans le raisonnement.

Exemples:
Démonstration de 2 = 1

L’expérience mentalisée:

Situation que l’on peut imaginer, mais difficilement concrétiser qui montre que des postulats conventionnels peuvent conduire à une absurdité. Ce type de paradoxe montre que le bon sens a tort.

Exemples:
Paradoxe de Galilée.

Le paradoxe authentique:

Ni faux raisonnement, ni " le bon sens a tort ", il défie toute résolution. Il est intrinsèque, sans réponse.

Voir Interdictions / Paradoxe du menteur

ONTOLOGIE

Ontologie: étude de la réalité la plus certaine. Étude des propriétés générales de tout ce qui est.

Peut-on, comme Euclide l’a fait en géométrie, déduire les théorèmes de la connaissance à partir d’un nombre limité d’axiomes.

Descartes s’y est essayé. Malheureusement, presque tous les énoncés concernant le monde réel sont, à un certain degré, douteux.

Exemples
Paris est la capitale de la France? Et s’il existait une vaste machination nous faisant croire que Paris est la capitale de la France!

Qui est le plus réel: le tyrannosaure ou le monstre du Loch Ness?

Qui nous dit que ce ne sont pas des savants fous qui, en stimulant votre cerveau, vous font croire que 2 + 2 = 4, alors que 2 + 2 = 650.

Notes:

L'ontologie est la branche de la philosophie qui traite de l'étude de l'être, de ses modalités, de ses propriétés.

En informatique, l'ontologie s'attache à la structuration de l'information. C'est une sorte de "grammaire" qui s'applique, non pas au langage, mais aux données.

SYLLOGISME

Syllogisme: un raisonnement sur le modèle suivant:

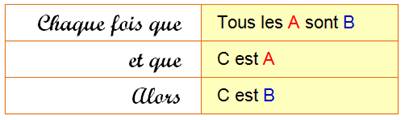
Exemples

Tous les hommes sont mortels.

Socrate est un homme.

Socrate est mortel.

Tous les banquiers sont riches.

Rockefeller est un banquier.

Rockefeller est riche.

Tous les corbeaux sont noirs.

L’oiseau dans " le corbeau " d’Edgar Poe est un corbeau.

L’oiseau dans " le corbeau " d’Edgar Poe est noir.

Un cheval bon marché est rare.

Tout ce qui est rare est cher.

Un cheval bon marché est cher!

Suite Tous les types de syllogismes

SORITE

Un sorite est une chaîne de syllogismes reliés entre eux, le prédicat de l’un devient le sujet de la suivante.

Exemple

Tous les corbeaux sont des corneilles.

Toutes les corneilles sont des oiseaux.

Tous les oiseaux sont des animaux.

Tous les animaux ont besoin d’oxygène.

Conclusion (évidente):

Tous les corbeaux ont besoin d’oxygène.

DÉDUCTION & INDUCTION
DÉDUCTION	INDUCTION
Façon logique de tirer des conclusions (ou vérités logiques) à partir d’hypothèses	Processus familier grâce auquel nous formons des généralisations
Syllogisme: Tous les hommes sont mortels Socrate est un homme. Donc Socrate est mortel.	Les corbeaux que j’ai observés sont noirs. Donc tous les corbeaux sont noirs
Hypothèses => VÉRITÉS LOGIQUES	FAITS => Généralisation de bon sens
Risque d’erreur sur les fondements de départ, mais la construction logique est solide.	Risque d’erreur dans le raisonnement, empirisme. Fondé sur la conviction que le monde n’est pas foncièrement trompeur
Le principe d’induction est toujours apparu moins légitime que celui de la déduction. Notez que l’on utilise le raisonnement inductif pour justifier le raisonnement inductif. On exprimer cette induction sur l'induction: " L’induction a soutenu l’épreuve du temps. Donc c’est un mode de raisonnement fiable". Paradoxe?!