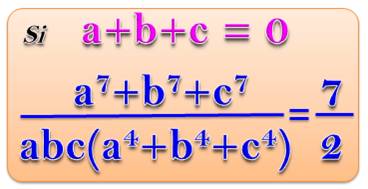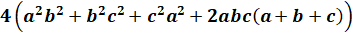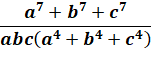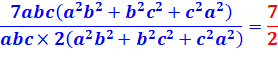|
||||||||||||||||||||||||||||||||||||||||||||
![]()
|
IDENTITÉ de degré 7 Cas particulier de résolution d'un
problème de degré 7. Présentation
d'après la démonstration décrite dans la vidéo en référence. |
|
|
||
|
Problème Avec la condition indiquée,
démontrer cette identité avec degré 7 au numérateur et degré 4 au
dénominateur. |
|
|
|
Tactique Développer
(a + b + c)k avec k
= 4 puis avec k = 3 pour atteindre le degré 7. Ces calculs produiront les puissances cherchées
(a7, b7, c7 …) et d'autres termes dont on
espère qu'ils vont se simplifier. |
Simplification Elle va naitre chaque fois que la somme (a + b +
c) sera en facteur, faisant tomber à zéro le terme où elle existe. |
|
|
|
|||
|
|
En tenant compte de (a + b + c) = 0. Premier cas significatif où cette propriété simplifie bien les choses ! |
||
|
|
= |
|
|
|
|
= |
Sous condition (a + b + c) = 0 |
|
|
|
|||
|
Calcul du carré qui est nul |
|
|
|
|
|
= |
|
|
|
|
= |
|
|
|
Encore au carré pour le degré 4 |
|
|
|
|
|
= |
|
|
|
|
= |
|
|
|
En rapprochant les deux |
|
|
|
|
|
= |
Sous condition (a + b + c) = 0 |
|
|
|
|||
|
Degré 7 |
|
Avec produit des dégrés 4 et 3 |
|
|
|
= |
|
|
|
|
= |
|
|
|
Cette factorisation est sans doute le point le plus délicat du calcul. |
= |
|
|
|
On a: a + b + c = 0; d'où ces remplacements. |
= |
|
|
|
Mise en facteur de abc |
= |
|
|
|
En rapprochant les valeurs de la ligne du haut et de celle du bas (avec
du bleu). |
|||
|
|
= |
Sous
condition (a + b + c) = 0 |
|
|
|
|||
|
Fraction |
|
Avec résulats obtenus pour le degré 7 et le degré 4 |
|
|
|
= |
Sous
condition (a + b + c) = 0 |
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()