Nombe d'or et les trois cercles

Édition du: 10/12/2024

INDEX Suite de Fibonacci et nombre d'or Géométrie Types de nombres	Nombre d'or
	Débutant	Valeurs	Phi et Fibonacci	Proportion
	Tout PHI en bref	Formules	Puissances	Construction
	Introduction	Fraction continue	Trigonométrie	Géométrie
	Historique	Phi et nombre 5	Trois cercles

Faites un double-clic pour un retour en haut de page

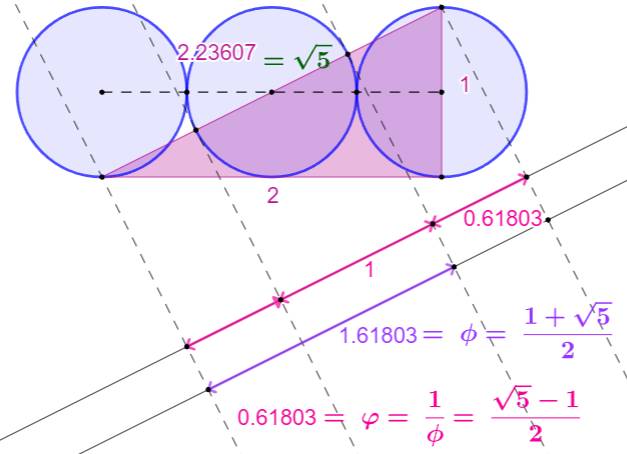
Nombre d'or et les trois cercles

Comment le nombre d'or se manifeste dans une figure comprenant trois cercles alignés et adjacents deux à deux.

Sommaire de cette page

>>> Le nombre d'or et les trois cercles

Débutants

Nombres

Glossaire

Nombres

Le nombre d'or et les trois cercles		haut

Construction Trois cercles dont les centres sont alignés et adjacents deux à deux. Le triangle rectangle rose dont deux sommets comme points de contact avec la tangente basse aux trois cercles; un sommet comme point de contact avec la tangente haute aux trois cercles. Alors, l'hypoténuse est divisée en segments représentant le nombre d'or et son inverse.	Explications Longueur de l'hypoténuse: h² = 2² + 1² = 5 et h = √5 L'hypoténuse passe par le centre du cercle central et le coupe selon un diamètre. Les deux autres segments sur l'hypoténuse sont égaux et chacun mesure:

Haut de page (ou double-clic)

Retour	Nombre d'or – Débutant Nombre d'or en bref Nombre d'or en géométrie Nombre d'or et le cercle
Suite	Nombre d'or – Introduction
Voir	Géométrie – Index
DicoNombre	Nombre 1,618…
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOr3Cer.htm