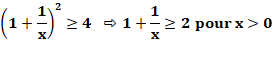|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DÉRIVÉE – Novices Vous savez ce qu'est une vitesse. Vous savez alors ce qu'est
une dérivée. Dérivée: taux de variation d'une grandeur. Vitesse: taux de variation de la distance
parcourue. Accélération: taux de
variation de la vitesse. Coucou! Je suis en première et je voudrais démarrer d'un bon pas >>> |
|
|
||
|
|
Ce
graphique montre la distance parcourue en fonction du temps. |
|
Note: Belle balade
durant laquelle j'aurais pu composer une jolie ballade
(poème épique) >>>
|
|
La
première heure, je vais plus vite que la seconde. La pente de la droite
témoigne de la vitesse. |
|
|
||
|
|
La
vitesse c'est la pente de la courbe. Mais quelle pente? |
|
|
Soit 100 = a . 22 Et a = 25
avec x = 1 => y = 25
est y' = 2 a x ici y' = 50 x
Elle
vaut 50 km/h au point x = 1 heure et elle vaut 100 km/h au point x = 2
heures. |
On note la distance en fonction du temps: d = f(t). Mais pour être plus général, nous allons prendre: y = f(x) Ici: y = 25 x² La dérivée est y' = 50 x Avec x = 1, y' = 50 km/h; C'est ma vitesse au temps 1 heure (droite tangente en vert). Avec x = 2, y' = 100 km/h; C'est ma vitesse au temps 2 heures (2e droite tangente en
vert). |
Voir Accélération
Vous ne l'avez pas demandé …
|
Je me pose une question Au
bout d'une heure, la vitesse
(instantanée) est déjà de 50 km/h, alors
que je n'ai parcouru que 25 km. Je trouve
cela bizarre. Voyons
cela en prenant une échelle de temps plus petite. Voyons
ce qui se passe toutes les cinq minutes. Explication Sur
ce tableau à gauche, les valeurs trouvées pour une heure
et deux heures de route. Notamment 25 km parcourus avec une vitesse au bout
d'une heure qui est grimpée à 50 km/h (sujet de notre interrogation).
Sur
le tableau à droite, le même type de calcul mais avec les minutes comme unité de temps. Nos valeurs au
bout d'une heure (60 min.) se retrouvent. Nous constatons que la vitesse
croit progressivement pour atteindre 50km/h. Calculons
la distance parcourue toutes les tranches de cinq minutes. Un calcul approximatif serait
le suivant: autour du temps 5 min, je prends la vitesse moyenne (0 + 4,17) /
2 = 2,08 que je multiplie par la tranche de temps de 5 min. soit 5/60 heure.
Résultat: 0,17. La somme de ces parcours élémentaires atteint les 25 km. Nous
voilà rassurés. |
|
|
||
|
6
fois plus en 1 heure, soit
60 km / heure. |
|
|
|
C'est vrai, alors, il faut mesurer pendant un tout petit intervalle
de temps pour éviter trop d'erreurs dues aux fluctuations de vitesse.
|
||
Merci à Valérie G. pour les conseils
d'amélioration
|
F
et F' sont sur un bateau. F tombe à l'eau. Que fait F'. Il dérive. |
Voir Pensées & humour
|
Problème Comment montre que la fonction f(x) = x + 1/x est
toujours supérieure ou égale à 2 pour tout nombre positif non nul ? Passage par un extremum Ayant appris la notion de dérivée, il est
possible de répondre à la question. Le minimum (ou le maximum) de cette
fonction sera atteint pour une dérivée nulle. Or, nous le verrons plus tard, la dérivée de
cette fonction est f'(x) = 1 – 1/x²
qui est nulle pour x = 1 et alors f(x) = 2. Pour x = 2, on a f(x) = 2 + 1/2 =
2,5 qui est plus grande et pour x = 1/2, f(x) = 1/2 + 2 = 2, 5 qui est aussi
plus grand. La fonction passe par un minimum pour x = 1 et f(x) est toujours
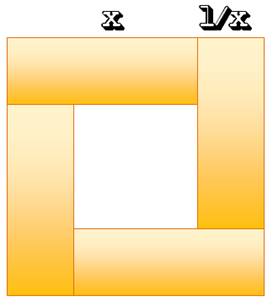
supérieure ou égale à 2. Le graphe de la fonction le montre. Solution imagée Sans recours aux dérivée, il astucieusement
possible de trouver le même résultat. L'idée consiste à utiliser la figure du carré à
droite. Son aire vaut: A = (x + 1/x)² L'aire des quatre rectangles vaut toujours 4 x 1
= 4. Et l'aire du carré lui est toujours supérieure (Aire du petit carré en
plus). Conclusion:
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
![]()