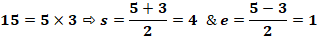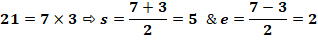|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
FACTORISATION des nombres différence de deux carrés Algorithme Une méthode originale proposée par Olivier Mehaye. Il s'agit
d'un algorithme de recherche d'un élément commun dans deux suites de nombres. Son fondement est exposé en Différence
des carrés de deux nombres et une approche avec des factorisations
particulières est expliquée en Factorisation. |
|
|
||||||||||||||||||||||||||||||
|
Une
approche originale de factorisation. |
Le but est de connaitre la factorisation de p = a.b Exemple avec p = 21 dont on cherche à trouver la factorisation: 3 x 7.
|
|||||||||||||||||||||||||||||
|
Procédé Former deux suites de nombre en choisissant p et
en faisant progresser n.
On repère le cas où T(n) = T'(m). C'est le cas pour n = 5 et m = 2 avec la
même valeur 46. La factorisation est simplement donnée par la
somme et la différence entre ces deux nombres. |
Formation des deux suites T et T'
46 = 21 + 5² = 2x21 + 2² Factorisation 21 = (5 – 2) (5 + 2) = 3 x 7 |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Cette
approche est astucieuse et marche pour presque tous les nombres. |
Une vérification par tableur semble montrer que l'on trouve toujours
une égalité et que: p = (n – m) (n + m) = s .
e |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
En fait, chercher
l'égalité revient à résoudre cette équation dont la solution s'exprime par le
produit d'une somme et d'une
différence des mêmes nombres. |
p + n² = 2p + m² n² – m² = p p = (n – m) (n + m) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Notez que
l'on n'a fait aucune hypothèse sur la nature du nombre p Le tableau montre les nombres p atteint par cette
relation entre m et n. Ils sont pairs comme impairs, mais … on y trouve:
Les nombres impairs y sont au moins une fois sur
la deuxième diagonale. Les nombres pairs multiples de 4, sauf 4, y sont
tous sur la troisième diagonale. Les autres pairs n'y sont jamais |
Table de p = (n – m) (n + m)
Les absents du tableau Les nombres pairs non multiples de 4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Théorèmes TOUT
nombre est égal à une différence de carrés, au moins. SAUF, les nombres en 4k
+ 2 et les nombres: 1, 2, 4. Conséquence TOUT
nombre impair, comme tout nombre premier (sauf 2), comme tout produit de
nombres premiers (sauf avec 2) sont:
|
p = n² – m² = (n – m) (n + m)
= s . e avec n = (s + e) /2 et m = (s – e) /2 Exemples
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||
|
L'idée
consiste à balayer deux listes jusqu'à détecter l'égalité entre deux
éléments. Hélas, il
n'existe pas de formule analytique directe qui donnerait les valeurs de m et
n, pas plus que celles des a et b. Une
méthode algorithmique s'impose. Le temps d'exploration restera néanmoins
important pour de grands nombres. D'autres méthodes
plus efficaces existent. |
Une implémentation sur tableur est possible, mais on s'intéresse
certainement à de grands nombres. La programmation est plus indiquée. |
||
|
Programmation Python
|
But Étant donné un nombre p, on se propose de trouver
sa factorisation en deux facteurs. Soit, trouver m et n et en déduire s et e: p (n – m) (n +
m) = s . e Commentaires On donne une valeur à p (volontairement un
produit à fin de test). On vérifie tout de suite que le nombre p n'est pas de
la forme 4k + 2. La liste T est ouverte. Elle mémorisera les éléments
de la liste qui croit le plus rapidement (n² + 2p). Boucle (for …)
qui calcule tt et t et conserve tt dans la liste T. Si la nouvelle valeur de t est déjà dans la liste
de tt, alors, on a trouvé notre égalité. Le nombre m est le rang de la valeur commune dans
la liste T. Les nombres cherchés sont n et m puis a et b. On imprime le résultat des recherches et on
stoppe la recherche avec un break. En bleu le résultat. |
||
|
Programmation Maple
|
But Identique Commentaires Initialisation par restart. Même commentaires que ci-dessus. Particularités On demande la factorisation avec ifactor à titre de test. Ajouter un élément à une liste se fait avec [op(liste), nouvel élément] L'instruction member
vérifie si un élément est dans la liste et en donne le rang en troisième
paramètre (ici: m). En bleu ce résultat. |
||
Voir Programmation – Index
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/P100a500/FactAlgo.htm
|
![]()