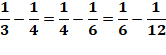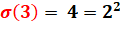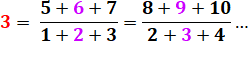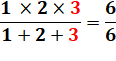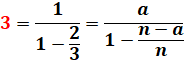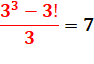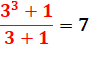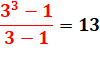Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 16/01/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	-0-	-1-		-2-	-3-		-4-	-5-	-6-	-7-	-8-	-9-

Nombre 3	Culture 3	Maths 3	De 3 à 3,9	Expressions en 3
Débutant 3	Culture 3 suite	Maths 3 suite	Cube	Proverbes avec 3
Quizz 3	Quantité 3	Divisibilité par 3	Puissance de 3	Sciences 3
Horloge maths	Trichotomie	Max avec trois 3	Multi-puissance 3

Trois

Three

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	11
Bases	/
Romain	III

Suite

Plus petit nombre dont la somme des diviseurs est un carré (4 = 2²).

Suivants: 22, 66, 70, 81, 94, 115, 119, 170, 210, 214, 217, 265, 282, 310, 322, 343, 345, 357, 364, 382, 385, 400, 472, 497, 510, …

Suite >>>

Caractérisation du nombre

Auto-nombre

Balancé

Chanceux d'Euler

Chanceux d'Ulam

Constructible

Cullen (1×2¹ + 1)

Dedekind

Déficient

Delannoy

Diédral parfait

Euclide premier

Factorielle double (3!! = 1·3)

Fermat premier

Fibonacci (4^e)

Fortuné

Hamilton

Heegner

Idonéal

Impair Le plus petit nombre premier impair

Jacobsthal

Jumeau avec 5, cousin avec 7

Lucas

Mersenne

Padovan

Paire de Wieferich

Perrin (2 fois)

Pi-premier

Premier (le seul suivant un premier)

Premier de Bertrand

Premier de Chen

Premier de Genocchi

Premier de Mersenne (2² – 1, le plus petit)

Premier de Pierpont

Premier régulier

Premier de Sophie Germain

Premier de Stern

Premier de Woodall (2 x 2¹ - 1)

Premier factoriel (2! + 1)

Premier faible

Premier jumeau (avec 5)

Premier horloge

Premier inévitable (ou minimal)

Premier minimal

Premier unique

Proth

Queneau

Stirling 1 et 2

Sylvester

Totient parfait

Ulam

Wieferich (paire avec 1006003)

Woodall (3 × 2³ – 1 = 23, premier)

Zuckerman

Géométrique

Triangle (le seul premier)

Seul premier suivi d'un carré

Pascal

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Préfixes diviseurs et multiplicateurs:

10^-3 milli

10 ³ kilo (mille)

Rappel Propriétés générales >>>

Un fou rentre chez lui. La pendule sonne trois fois. Oh, ça va! Je sais qu'il est une heure, pas la peine de le répéter trois fois!

Le couple à trois est fréquent, mais généralement deux seulement sont au courant – Rapporté par Isabelle Mergault.

Voir Pensées & humour

PROPRIÉTÉS MATHÉMATIQUES générales

Compter	1, 2, 3 partez Bon, à trois, on y va!	>>>
Numération	Bloc de trois chiffres pour la lisibilité des nombres.	>>>
Jeux	Le plus petit carré magique est d'ordre 3, additif comme multiplicatif	>>>
	Bachet a montré qu'on peut effectuer toutes les pesées avec des poids triples, en utilisant les deux plateaux d'une balance.	>>>
	Le 3, associé au 5, est l'objet de l'énigme dite de Sherlock Holmes.	>>>
	Comment 3 devient 4 (en conservant trois barres).	>>>
	Énigme des trois maisons: eau, gaz et électricité	>>>

Calcul	Tout nombre dont la somme des chiffres est divisible par 3, est divisible par 3. Soit un couple de nombres, leur somme et leur différence, alors, l'un des quatre est divisible par 3.	>>>
Algèbre	Histoire de la résolution des équations du troisième degré.	>>>
	Comparaison ternaire entre deux nombres a et b: a < b ; a = b ; a > b
Logique	Le tiers exclus (troisième possibilité exclue). Les trois principes logiques.	>>>
Th. des Nbs	Tout nombre est la somme d'au plus trois nombres triangulaires – Gauss.
	Conjectures de Goldbach Tout entier (≥ 6) est la somme de trois nombres premiers. Tout nombre impair (≥ 7) est la somme d'au plus trois nombres premiers.	>>>
	La somme des inverses des carrés des nombres impairs est égale à trois fois celle pour les nombres pairs	>>>
	Tout nombre est la somme de trois palindromes en base b (b > 4) et quatre à partir de b = 2.	>>>
	Théorème de Fermat-Willes L'équation a^3 + b^3 = c^3 n'a pas de solution en nombres entiers. Conjecture de Beal L'équation a^x + b^y = c^z n'a pas de solution si (a, b, c) sont des entiers premiers entre eux et si (x, y, z) sont des entiers supérieurs à 2.	>>>
Th. Chaos	Un système dynamique à une dimension, avec un cycle de période trois, contient aussi toutes les autres périodes.	>>>

Géométrie	Trois points définissent un plan. Trois pieds à une table lui assurent la meilleure stabilité, c’est plus difficile avec quatre.	>>>
	Trois côtés, trois angles: le triangle. Le triangle est constructible à la règle et au compas.	>>>
	Quatre jeux de trois droites remarquables dans le triangle: hauteurs, médianes, médiatrices et bissectrices.	>>>
	Trisectrices et théorème de Morley dans le triangle	>>>
	Trois types de géométrie plane ou euclidienne, hyperbolique et sphérique. Trois variétés primaires en dimension 2 (topologie).	>>> >>>
	3D ou les trois dimensions géométriques de notre monde. Symbole de vision en relief.	>>>
	r = 3 rayon du cercle inscrit dans le triangle de Pythagore (7, 24, 25)	>>>
	1, 2, 3 Ratio entre volumes des cônes, demi-sphère et cylindres.	>>>
	Trisection de l'angle. Impossible à la règle et au compas. Faisable avec une équerre.	>>>
	Trisection du segment: toutes les méthodes avec démonstrations.	>>>
	Partage du rectangle en trois triangles possible sous conditions	>>>
	Théorème des trois perpendiculaires.	>>>
	Théorème des trois cercles de Monge	>>>
	Trois pavages du plan par des polygones. Trois pavages quasi-périodiques de Penrose.	>>>
	Trois formes étoilées du dodécaèdre.	>>>
	La Bible indique que la valeur de serait 3.	>>>
	L'aire de la cycloïde est égale à trois fois celle du disque qui l'a engendrée.	>>>

Suite Géométrie en 3

PROPRIÉTÉS MATHÉMATIQUES détaillées

Chiffres et numération

3	N'est repdigit dans aucune base. Il n'est pas brésilien.

Type séquence

1, 3, 6, 10, …	3, comme 2 et 1, fait encore partie du départ de nombreuses séquences de nombres, comme les nombres triangulaires.
1, 11, 21, 1211, 111221, 312111, …	La séquence mystérieuse dite du "commentaire numérique" semble être limité aux trois seuls chiffres 1, 2 et 3.
3, 5, 7	Seul triplet de nombres premiers.
3, 4, 6, 12	Quadruplet harmonique, le plus petit.

Addition

3 = 1 + 1 + 1 = 2 + 1 = 3	Les trois partitions du nombre 3.
3 = 1 + 2 = 1! + 2!	Seul à être somme de tous ses prédécesseurs comme de la somme des factorielles de ses prédécesseurs Partition unique avec deux chiffres différents. Nombre triangle. Nombre de Fibonacci (1, 3, 4, 7, 11, 18, 29...).

Soustraction

3 = 7 – 4 33 = 7² – 4² …

Motifs produisant une persistance du 3.

Table de multiplication du 3

Voir Table complète

Multiplication

	Premier nombre qui augmente plus par multiplication que par addition. 3 + 3 = 6 et 3 x 3 = 9
2 × 3 – 1 premier	Primorielle – 1 première, la plus petite.

Division et diviseurs

= 1 + 3	La somme des diviseurs est un carré. Le plus petit (hors 1).
	Comment faire 3 avec des puissances de 2.
	Motif général dont le résultat est la division des termes centraux.
		Motif général
	Deux seules divisions pannumériques avec quotient égal à 3.
123 = 3 x 41 divisible par 3 1 + 2 + 3 = 6 divisible par 3	Un nombre est divisible par 3 si la somme de ses chiffres est divisible par 3.
3 = 1^1 + 2^1 = 1 x 3	Somme d'une puissance de nombres consécutifs, divisible par le nombre suivant (Propriété générale).
3 = 3 / 3 + (3+3) / 3	Faire 3 avec k chiffres identiques.
2^2 – 1 = 3 2^4 – 1 = 15 2^6 – 1 = 63 2^8 – 1 = 255 …	Toutes les puissances paires de 2, moins 1, sont divisibles par 3.
3 => Fréquence = 1/6	Deuxième nombre premier. Plus petit nombre premier impair Deuxième facteur le plus fréquent avec une fréquence de 1/6.
3, 5 5, 7 11, 13	Premier couple de premiers jumeaux. À l'exception de (3,5), ils sont tous de la forme 6n ± 1
3	Seul premier p tel que p-1 soit premier. Seul premier p qui divise 2^p + 1. Seul premier de la forme n² - 1.
(2^2n – 1) 0 mod 3 (2^2n – 1) 3 mod 6	Divisibilité des nombres de Mersenne composés avec puissance paire.
3	Divise tout nombre de la forme n^3 – n = (n–1) n (n+1) produit de trois nombres consécutifs. Divise tout nombre de la forme ab ( a² – b² )
3 = n.m / (n + m)	Pour deux couples de nombres seulement.
3 n² + 1	Carré plus un jamais divisible par 3.
3, [4, 49] 4 = 2² et 5 = 5 => 5 – 2 = 3 49 = 7² et 50 = 2x5² => 10 – 7 = 3	Plus petit écart entre radicaux de nombres successifs, lesquels sont (4, 5) et (49, 50).

Puissance

Voir Puissance / Racine

a^3 = a . a . a 0^3 = 0 mais 3^0 = 1 1^3 = 1 / 2^3 = 8 / 3^3 = 27 / …	Un nombre à la puissance 3 est un cube.
3 = 2^2 – 1	Plus petit nombre de Mersenne premier.
3 = 2^2 – 1^0	Plus petite différence de deux carrés. Propriété générale des nombres impairs: différence des carrés de deux nombres consécutifs.
3 = 2 + 1 = 2² – 1²	Motif valable pour tout nombre impair.
3 = 1^0 + 1^1 + 1^2 = 1^1 + 1^2 + 1^3 = 1^a + 1^b + 1^c	Somme des puissances successives de 1.
3 = 2^1 + 1 = 2^2 à la puissance 0 + 1	Plus petit nombre de Fermat. Plus petit Fermat premier (Rappel 2^0 = 1).
3 = 1^3 + 1^3 + 1^3 = 4^3 + 4^3 + (–5)^3 = 128 – 125 3 = 569936821221962380720^3 + (-569936821113563493509)^3 + (-472715493453327032)^3	Trois seules possibilités connues pour somme de trois cubes. La troisième somme est due à Booker et Sutherland en 2019.
3 = 2^7 – 5^3 = 128 – 125	Différence entre puissances (seule différence égale à 3 jusqu'à un million et sans doute au-delà).
	Racines continues.
	Nombre d'or à la puissance 5.

Nombre et ses puissances

	§ Racines avec décimales proches à 0,00008… près.
x^x = 27 => x = 3	§ Racine de cette équation.

Voir Racine de 3

Sommes des chiffres des puissances identiques

3^2 = 9	9	3^6 =729	7+2+9 = 18	3^9 =19 683	1+9+6+8+3 = 27
3^3 = 27	2+7 = 9	3^7 = 2 187	2+1+8+7 = 18	3^10 = 59 049	5+9+0+4+9 = 27
3^4 = 81	8+1 = 9	3^8 = 6 561	6+5+6+1 = 18
3^5 = 243	2+4+3 = 9

Voir Tables de telles relations

Les nombres 3, 4, 5 et 6 avec des carrés et des cubes
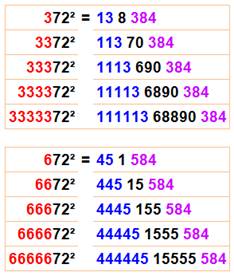
3² + 4² = 5² Aire = 3x4 / 2 = 6 9 + 16 = 25 33² + 44² + 55² 333² + 444² + 555² …	Triplet de Pythagore remarquable: trois nombres consécutifs. Triplets sacré ou isiaque. Les multiples sont également des triplets de Pythagore.
3^3 + 4^3 + 5^3 = 6^3 27 + 64 +125 =216	Somme remarquable de cubes.

3^2 = 1 + 3 + 5 = 9 3^3 = 7 + 9 + 11 = 27 ²	Somme de six nombres impairs. Voir Impairs, carrés et cubes / Belles formules
3^0 = 1 3^2 = 2 + 3 + 4 = 9 3^4 = 5 + 6 + 7 + … + 12 + 13 = 81 3^6 = 14 + 15 + 16 +...+ 39 + 40 = 729	Motif général. La quantité de termes est 1, 3, 9, 27...
3^6 = 729 3^2 = 9 3^3 = 27	Curiosité et moyen de retenir cette puissance.
3^2 – 1 = 8 3^4 – 1 = 80 3^6 – 1 = 728 3^8 – 1 = 6560 …	Toutes les puissances paires de 3, moins 1, sont divisibles par 8. Sinon (impair): divisible par 2.
3^0 + 3^1 + 3^2 + 3^3+ 3^4 = 11² = 121	121 est la somme des diviseurs de 3^4 et cette somme est donc un carré. C'est le seul nombre premier présentant cette propriété.
	Bicarré concaténation de deux cubes.
3^n | 33…3n	Un repdigit de 3n chiffres est divisible par 3^n
1^3+ 2^3+ 3^3 = (1 + 2 + 3)² = 36	Somme des n premiers cubes est un carré.
3 x 2^3 – 1 = 23 = nombre premier	Générateur de nombre de Woodal (2^e).
3^2 = 1^k + 2^3 3^4 = 2^5 + 7^2	Puissance = somme de puissances.
3 = 2^7 – 5^3 = 128 – 125 3 = 2^2 – 1^k = 4 – 1 (trivial)	Cas rare de différence de puissances égale à 3, hors cas triviaux. Seule?
3² – 1 = 9 – 1 = 2^3	Premier nombre puissant en n² – 1. Liste: 3, 17, 26, 99, 485, 577, 1351, …

Factorielles

3 = 4! / 2^3 = 24 / 8	Factorielle divisée.
	Somme des nombres qui divise la factorielle.
3 = 1! + 2!	Le seul à être la somme des factorielles des nombres qui le précédent
3! + 1 = 7	Factorielle plus 1 donne un nombre premier.
3! – 1 = 5 & 3! + 1 = 7 3! – 3 = 3 2! + 1 = 3	Générateurs de nombres premiers factoriels. Seule forme en n! – n qui donne un premier. Nombre premier factoriel.
1! + 2! + 3! + 4! = 33	Toutes les sommes de factorielles à partir de là se terminent par 3.

Autour de ce nombre

- 3

Nombre de Heegner.

Comment écrire 3 avec seulement les nombres 1, 2 et 3 ? Cas particulier d'une écrire possible des nombres en fractions.

Il existe d'autres possibilités, objet de jeux avec les nombres.

Tout nombre entier peut être exprimé avec les log. Voir problème des quatre 4.

1/3 = 0,333 …

2/3 = 0,666 …

3/3 = 1

Seul nombre premier de période 1. Nombre premier unique.

Les nombres divisés par trois sont:

soit périodique avec 3 pour décimale,

soit périodique avec 6 pour décimale,

soit entiers (divisible par 3).

3 + 2³ = 11

Motif

On retrouve ces motifs pour tous les nombres de la forme :

En 3	En 6	En 9
3n A	6m B	9p C

Répétition de 3, 6 ou 9 en nombre quelconque suivi d'un nombre quelconque

Exemple

3² = 9 3⁷ = 2 187

3³ = 27 3⁸ = 6 561

3⁴ = 81 3¹⁰ = 59 049

3⁶ = 729 3¹¹ = 177 147

Jamais de chiffre 3 dans toutes ces puissances de 3.

3² = 2 x 2² + 1

9 = 2 x 4 + 1

Une des solutions de l'équation de Pell-Fermat: x² – 2y² = 1.

§ Le deuxième nombre premier de cette forme.

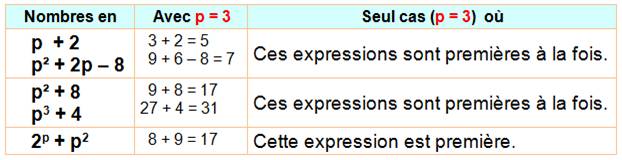
§ Nombre premier. Expression première pour: 3, 5, 7, 71, 151, 157 (testée jusqu'à 1000).

p = 3 est premier et la fraction est un nombre entier et premier.

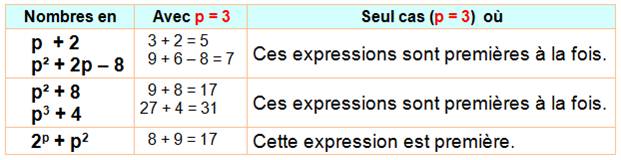
Seuls tels nombres avec p = (3, 5, 17 et 157).

p = 3 est premier et la fraction est un nombre entier et premier.

Liste de tels nombres avec p = (2, 3, 19, 31, ?).

§ Somme des chiffres nⁿ divisible par n.

Liste: 1, 2, 3, 9, 18, 27, 54, 90, 108, 163, 197, 254, 432, 1292, 2202, 9648, … OEIS A108827

Puissance Pi proche de l'entier 31.

3 | 10 ³⁺¹ – 1

§ Cas de divisibilité aussi observé pour: 3, 9, 11, 33, 77, 99, 143, 303, 369, 407, 707, 959, 1001, …

Jeux et curiosités

3 x 1 035 = 3 105 3 x 2 474 = 7 422 3 x 2 475 = 7 425 3 x 10 035 = 30 105 3 x 10 350 = 31 050	3 x 10 351 = 31 053 3 x 12 375 = 37 125 3 x 14 247 = 42 741 3 x 14 724 = 44 172 …		Produits qui conservent les chiffres. À noter: 3 x 2575 = 7725 3 x 10335 = 31005 3 x 11035 = 33105
3! = 3 x 2 x 1 = 3 + 2 + 1 = 6		Factorielle aussi égale à la somme de ses facteurs.
		Jeu du quatre 4.

3,14 … nombre Pi et autres nombres avec 3 et décimales >>>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]	Repdigit (Brésilien)
2, [1, 1] 3, [1, 0]	2, [1, 1]

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page Nombre 3 en maths – Suite
Voir	Dualité Numération (binaire et autres)
Site	Références Internet
Cette page	http://villemin.gerard.free.fr/NombDico/TroiP1n3.htm