Triangle dans un rectangle

Édition du: 08/02/2025

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Double triangle rectangle
	Nappe sur table	Triangle rectangle partagé	Rectangle et triangle
	Carré oblique	Carré et triangle équil.	Triangles dans triangle
	Triangle dans quadrilatère	Trapèze et triangle	Trois triangles réunis
	Triangle – Divers

TRIANGLES

Florilège de défis

Quelques défis simples de géométrie. Impliquant principalement le triangle.

Sommaire de cette page

>>> Deux triangles alignés

>>> Deux triangles posés l'un sur l'autre

>>> Triangle rectangle et sa hauteur

>>> Triangle avec deux côtés et une hauteur

>>> Triangle et médiatrices

>>> Triangle et son ellipse inscrite

Débutants

Géométrie

Glossaire

Géométrie

Deux triangles alignés		haut
Simple calcul d'angles avec triangles remarquables.
Construction Un triangle équilatéral et un triangle isocèle alignés. L'angle au sommet du triangle isocèle vaut alpha et l'angle entre les deux triangles vaut 2 alpha. Quelle est la valeur de l'angle alpha ? Piste Évaluation de l'angle plat formé par la droite d'alignement des deux triangles. Angle de 60° du triangle équilatéral, Angle 2α, Angle à la base du triangle isocèle, sachant que la somme des deux vaut 180 – α. Calculs	Figure

Deux triangles posés l'un sur l'autre		haut
À nouveau un calcul d'angles avec triangles remarquables.
Construction Un triangle rectangle isocèle (bleu) et, posé sur lui, un triangle isocèle (vert). Valeurs de l'angle x ? Piste Dans le triangle rectangle isocèle, les deux angles à la base valent 45°. Calculs	Figure

Triangle rectangle et sa hauteur		haut
Application de la propriété de la hauteur des triangles rectangles.
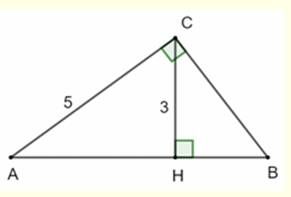
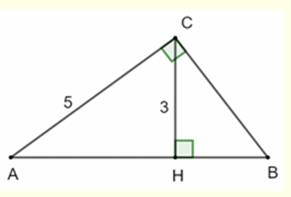
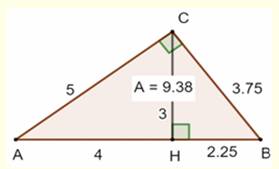
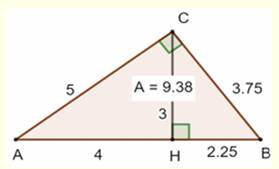
Construction Un triangle rectangle dont un côté de l'angle droit mesure 5 cm et la hauteur 3 cm. Résoudre le triangle ABC. Piste Le triangle rectangle ACH est le triangle bien connu (3, 4, 5) et AH = 4 . La hauteur est liée aux segments qu'elle découpe selon : CH² = AH . HB Calculs 3² = 4 . HB => HB = 9/4 = 2,25 cm BC² = 3² + (9/4)² = 225/16 => BC = 3,75 cm Aire triangle ABC : ½ x 5 x 3,75 = 9,375 cm²	Figure initiale Figure avec notations

Triangle avec deux côtés et une hauteur		haut
Application de la propriété du triangle inscrit dans un demi-cercle: c'est un triangle rectangle.
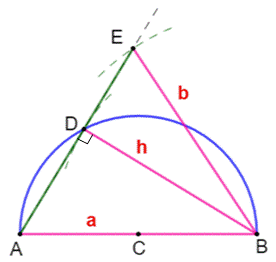
Question Construire un triangle dont on connaît la longueur de trois segments (roses) issus d'un sommet (ici: B): deux côtés (a et b) et la hauteur (h). Construction Demi-cercle de diamètre a. Cercle de rayon h et de centre B. Intersection en D. Demi-droite AD. Cercle de rayon b et de centre B. Intersection en E. Le triangle ABE est le triangle demandé.	Figure avec construction

Triangle et médiatrices		haut
Une construction du triangle à partir de ses trois médiatrices.
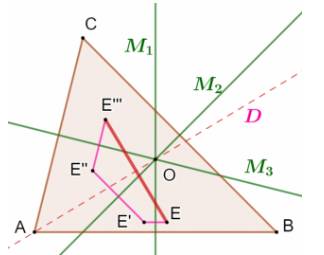
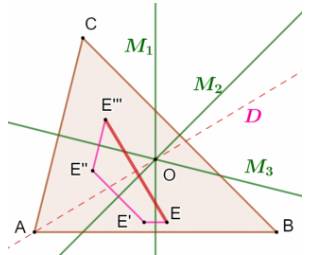
Question On connaît les médiatrices M₁, M₂ et M₃ d'un triangle. Construire un triangle ABC ayant ces médiatrices. Construction Choisir un point E quelconque. Construire les symétriques E', E'' et E''' par rapport aux trois médiatrices. La nouvelle médiatrice D de EE''' passe par le point O et surtout, elle passe par un des sommets du triangle. Disons A, un point sur D. Même chose pour construire les points B et C par rapport aux deux autres nouvelles médiatrices. Le triangle ABC est le triangle demandé.	Figure avec construction

Triangle et son ellipse inscrite		haut
Construction de l'ellipse inscrite dans un triangle basée sur la propriété du cercle directeur de l'ellipse.
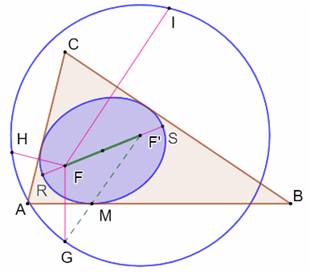
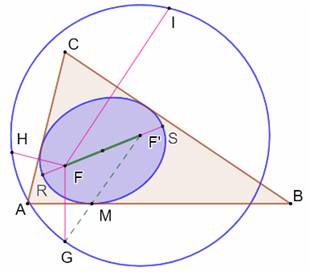
Ellipse Construire une ellipse inscrite dans le triangle quelconque ABC, étant donné l'un des foyers F (un point quelconque interne au triangle). Notez que selon la position du foyer F, il y a une infinité d’ellipses inscrites dans le triangle ABC. Construction Construire les points G, H et I qui sont les points symétriques du point F par rapport aux côtés du triangle. Le cercle passant par ces trois points est le cercle directeur de l'ellipse. Le centre F' du cercle est le second foyer de l'ellipse. Joindre ce foyer F' à l'un des points du cercle, disons G. Intersection en M avec AB. Construire l'ellipse avec pour foyers F et F' et passant par le point M. Les logiciels de dessin comme GeoGebra savent réaliser ce type de tracé. Sinon tracer le lieu des points tels que MF + MF' = RS = F'G = R = constante. Notez que : FM = MG.	Ellipse de foyer F inscrite dans le triangle ABC Propriété Le cercle directeur de l'ellipse de foyers FF' a pour rayon le grand axe RS de l'ellipse. Ce cercle est centré soit sur F soit sur F'. Les points symétriques de l'un des foyers sont sur le cercle directeur centré sur l'autre foyer.

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x⁴ Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/TrgDiv.htm