Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 11/02/2022 M'écrire Brèves de Maths

INDEX Courbes Géométrie	ELLIPSES
	Coniques	Ellipse	Ovale	Propriétés diverses
	Construction	Son périmètre		Quart d'ellipse

Ellipse – Propriétés diverses Propriétés et curiosités à propos des ellipses; énigmes.
et plus	Sommaire de cette page >>> Le lieu est une ellipse >>> Point de Frégier >>> Théorème de Brianchon >>> Théorème de Pascal	Débutants Géométrie Glossaire Géométrie

Le lieu est une ellipse

haut

Problème

Une collection de segments de longueur 4.

Une extrémité de ces segments est située sur la droite y = x et l'autre sur la droite y = 2x.

Donner l'équation du lieu des points milieux de ces segments.

Solution

On choisit un point sur chaque droite :

A(a, a) sur la droite y = x

B(b, 2b) sur la droite y = 2x

Coordonnées du milieu du segment AB, et déduction des valeurs de a et b:

2x = a + b	2y = a + 2b
2y – 2x = b	4x – 2y = a
b = 2(y – x)	a = 2(2x – y)

Or, le segment AB mesure 4 unités, et avec le théorème de Pythagore :

(a – b)² + (2a – b)² = 4²

a² – 2ab + b² + 4a² – 4ab + b² = 16

5a² – 6ab + 2b² = 16

Figure

En vert les deux droites. On a prit y = x et y = 10 x pour une meilleure lisibilité.

Un point glissant sur l'une d'elle.

Un cercle centré sur ce point glissant de diamètre 4. Les deux intersections avec l'autre droite verte.

Les points milieux dont on observe la trace elliptique en rose.

En remplaçant a et b:

Cette équation en y² et x² est celle d'une ellipse.

5(2(y – x))² – 6(2(y – x))(2(2x – y) ) + 2(2(2x – y) )² = 16

20(y² – 2xy + x²) – 24(2xy – y² – 2x² + xy) + 8(4x² – 4xy + y²) = 16

(20 + 24 + 8)y² – (40 + 72 + 32)xy + (20 + 48 + 32)x² = 16

52y² – 144xy + 100x² = 16

13y² – 36xy + 25x² = 4

Point de Frégier		haut
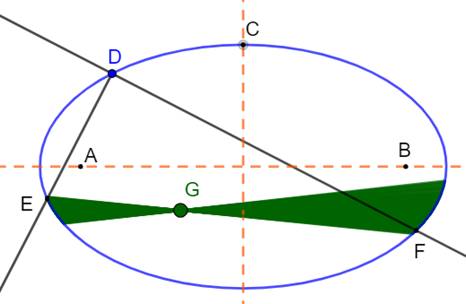
Toutes les cordes EF de l'ellipse, telles que l'angle en D est droit, passent par un même point fixe G. Théorème Soit une conique et D un point de cette conique. Toutes les cordes de la conique vues sous un angle droit depuis D sont sécantes en un même point G.

Théorème de Brianchon		haut
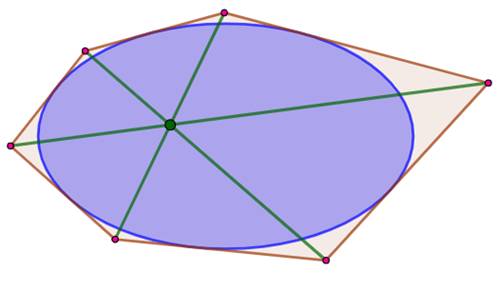
Une ellipse et six points. Les tangentes en ces points. Théorème Les trois droites passant par les intersections opposées des tangentes sont concourantes.

Voir Théorème de Brianchon

Théorème de Pascal		haut
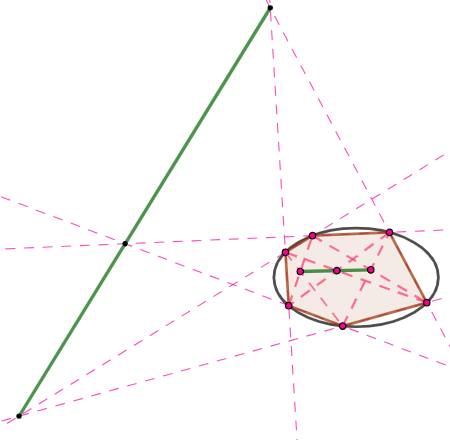
Une ellipse et six points. Les six cordes prolongées passant par deux points adjacents. Théorème Il existe trois intersections qui sont colinéaires. Les "diagonales" internes à l'ellipse. Théorème Il existe trois intersections qui sont colinéaires. Théorème de Pascal et théorème de Brianchon sont le dual l'un de l'autre.

Voir Étoile mystérieuse de Pascal ou hexagone mystique / Pascal et les coniques

Haut de page

Retour	Ellipse
Suite	Calcul du périmètre de l'ellipse Cercle inscrit dans le quart d'ellipse Cône elliptique – Développements Ellipse dorée Étoile mystérieuse de Pascal ou hexagone mystique Ovale – Ove
Voir	Courbes élémentaires Courbes elliptiques DicoMot Géométrie – Débutants Géométrie – Glossaire Géométrie – Index Lois de Kepler
Site	Théorème de Brianchon – Wikpédia Hexagone mystique – Bibm@th Théorème de Brianchon – Bibm@th Ellipses: Incircle and Circumcircle
Cette page	http://villemin.gerard.free.fr/Geometri/Coniques/Ellipse1.htm