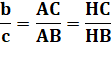construction du triangle à partir de ses bissectrices

Édition du: 25/01/2021

INDEX Triangles Constructions Géométrie	CONSTRUCTION – TRIANGLE
	Types de triangles	Constructions élémentaires des triangles			Quadrature
	*Constructions*	Orientation	LLL	AAA	LAL …
	*Constructions*	Général	hhh	bbb	Centres
	Résol. des triangles	Quelconque	mmm	MMM	Milieu

L: côté; A: Angle; h: hauteur; m: médiane; M: médiatrice; b: bissectrice

Construction des triangles

connaissant les BISSECTRICES

Comment dessiner un triangle à partir de ses trois bissectrices ?

Construction à partir de la connaissance de:

leurs directions,

leurs longueurs, ou leurs pieds: ces cas sont en général impossibles à résoudre.

Sommaire de cette page

>>> Les angles du triangle

>>> Construction des angles du triangle

>>> Construction du triangle avec les angles des bissectrices

>>> Construction avec trois longueurs : 2 côtés + 1 bissectrice

Débutants

Triangle

Glossaire

Triangle

Anglais: Triangle (location) construction problems

Les angles du triangle et ceux des bissectrices
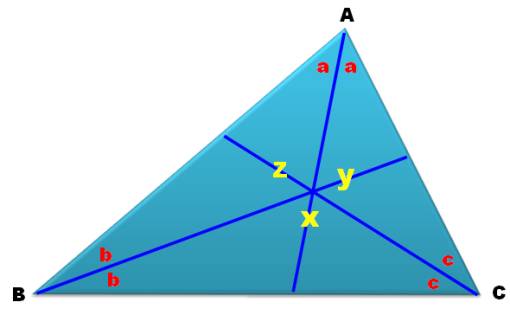
Cas où on connait:	Les trois angles entre les bissectrices, ou, Le tracé des droites portant les bissectrices.
X = 180 – b – c 2a + 2b + 2c = 180 b + c = 90 – a X = 90 + a a = X – 90 b= Y – 90 c = Z – 90

Construction des angles du triangle
Compte tenu de ces trois relations, la construction revient à celle d'un triangle dont on connait les trois angles. Nous disposons donc des trois droites bissectrices et d'un sommet A. Construire le triangle.
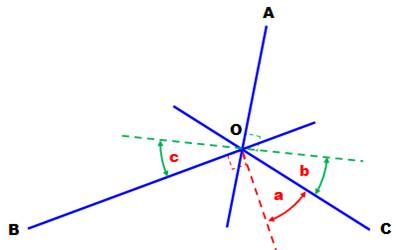
Construction des angles a, b et c Pour information, car seul a est utile. Rappel: a = X – 90° = ^BOC – 90°

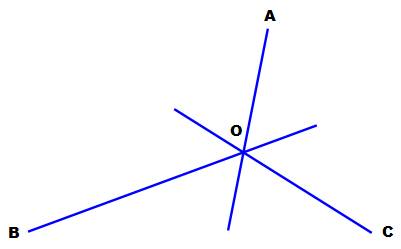
Construction du triangle de sommet A
Les trois bissectrices en bleu. Le sommet A. Construction de l'angle a On va construire le triangle isocèle ocre en O et le reporter en A.
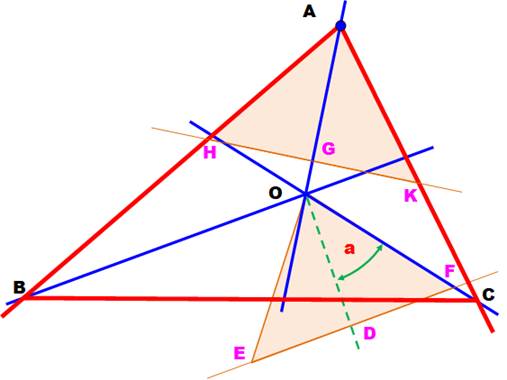
Un point quelconque D sur la perpendiculaire verte. Perpendiculaire en D à la droite verte. Intersection F. Cercle (D, DF). Intersection E. Création du triangle isocèle OEF.		Cercle (A, OD). Intersection G. Perpendiculaire en G à AO. Cercle (G, DF): intersections H et K. Création du triangle AHK. Angle en A = 2a. Intersections B et C de AH et AK avec les bissectrices, créant les deux autres sommets.

Trois longueurs : 2 côtés + 1 bissectrice
Cas où on connait:	La longueur de deux côtés et Celle de la bissectrice de l'angle commun.
Données d: longueur de la bissectrice b et c: longueurs des côtés Idée Construire le triangle ABC avec AH la bissectrice de l'angle A. D'après le théorème de la bissectrice, on doit avoir:
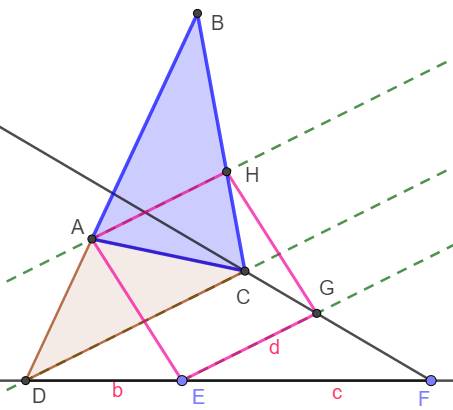
Construction	Points alignés DEF tels que DE = b et EF = c Parallèles en D et E selon un angle au choix. Point G tel que EG = d Intersection C de FG ave parallèle en D. Triangle isocèle: base DC et côtés de longueurs b. Parallèle en A à DC. Point H tel que AH = d: c'est notre bissectrice. Point B, intercetion de DA et CH. ABC est notre triangle.
Justification	AH = EG = d du fait de la construction. AC = DE = b, aussi

Impossibilité

Impossible de construire un triangle isocèle à partir des longueurs de deux bissectrices (sauf cas du triangle équilatéral).

Merci à Jean Jacques Alliot pour l'idée de cette page

Retour	Construction du triangle quelconque Construction à partir de certains centres
Voir	Aire égale pour trois triangles dans un rectangle Allumettes Angle Carrés Centre de gravité Cercles Droite Égalités des triangles Jeux Polygones Probabilité d'obtenir un triangle obtusangle Quadrupler le triangle Résolution du triangle quelconque Symétries Triangle – Index Triangle de Pythagore Types de triangles
Site	Construct a Triangle Given the Lengths of Two Sides and the Bisector of Their Common Angle – Wolfram Triangle From Angle Bisectors – Cut-the-knot – Vladimir Zajic Conic Construction of a Triangle from the Feet of Its Angle Bisectors – Paul Yiu
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Construc/ConsBiss.htm