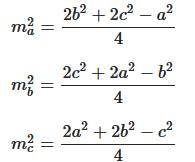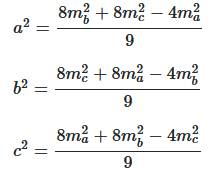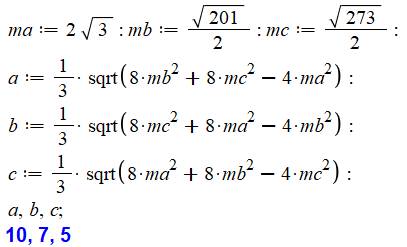Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 25/01/2021 M'écrire Brèves de Maths

INDEX Triangles Constructions Géométrie	CONSTRUCTION – TRIANGLE
	Types de triangles	Constructions élémentaires des triangles			Quadrature
	Constructions	Orientation	LLL	AAA	LAL …
		Général	hhh	bbb	Centres
	Résol. des triangles	Quelconque	mmm	MMM	Milieu

L: côté; A: Angle; h: hauteur; m: médiane; M: médiatrice; b: bissectrice

Construction des triangles connaissant les MÉDIANES Construire le triangle connaissant les médianes d'une manière ou d'une autre.
	Sommaire de cette page >>> Types de constructions >>> Pied des médianes >>> Méthode des longueurs >>> Méthode du parallélogramme >>> Méthode des trisections	Débutants Triangle Glossaire Triangle

Anglais: Triangle (location) construction problems

Types de constructions		haut
Cette page couvre la construction des triangles dont on connait les médianes.	Trois cas possibles. On connait: leurs longueurs, ou leurs directions, ou leurs pieds.

Pieds des médianes		haut
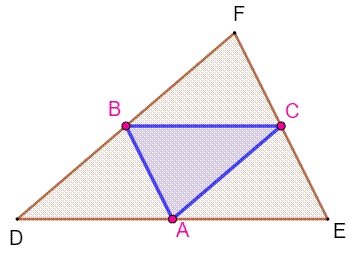
But On connait les trois pieds des médianes A, B, C. Tracer le triangle origine DEF. Si on connait les directions des trois médianes, on connait les trois points d'intersection. Construction 1. Tracer le triangle médian (bleu) 2. Parallèles en A, B et C au côté opposé. Intersections D, E et F.

Voir Autre méthode

Construction (AMa, BMb, CMc) – Méthode des longueurs		haut
Calcul Formules des médianes et calcul des longueurs des côtés en fonction de celles des médianes. Construction 3. Calculer les valeurs de an b et c. 4. Construire le triangle ABC.
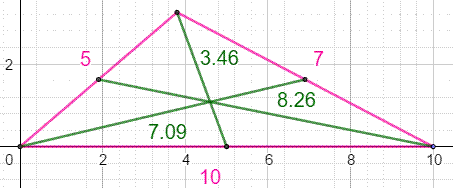
Exemple Longueurs des médianes: ma = 2 rac(3) = 3,46 mb = 1/5 rac(201) = 7,09 mc = 1/2 rac(273) = 8,26 Longueur des côtés: a = 10 b = 7 c = 5	Calcul Illustration

Construction (AMa, BMb, CMc) – Méthode du parallélogramme		haut
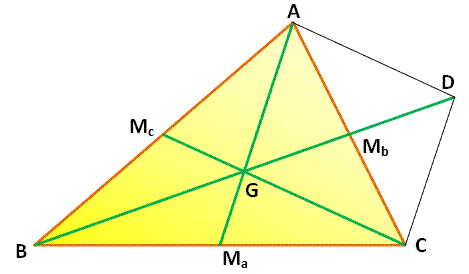
Problème Construire le triangle (jaune) dont on connait la longueur des trois médianes (en vert). Propriétés L'astuce consiste à construire le parallélogramme AGCD. Alors le triangle AGD est connu: AG = 2/3 AMa AD = GC = 2/3 CMc GD = BG = 2/3 BMb
Note au sujet des 2/3 Prolonger BMb d'une longueur égale à GMb est, en fait, le moyen habituel pour démontrer que le centre de gravité coupe la médiane aux deux tiers.	On prolonge BMb tel que GMb = MbD. Par construction AMb = MbC. Le quadrilatère ADCG, dont les diagonales se coupent en leur milieu, est un parallélogramme. Les côtés opposés sont parallèles. Dans le triangle ABD: AD est parallèle à GMc et AMc = McB. Alors: BG = GD = 2 GMb
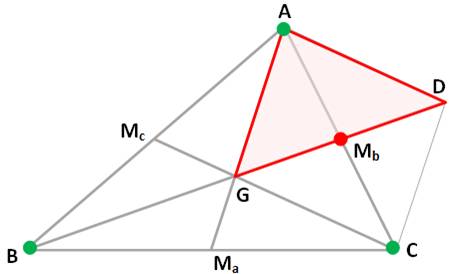
Construction 5. Calculer les longueurs des trois segments AG, AD et GD (2/3 des médianes connues). 6. Construire le triangle ADG. 7. Point Mb milieu de DG. 8. Point C, symétrique de A par rapport à Mb. 9. Point B, symétrique de D par rapport à G.

Construction (AMa, BMb, CMc) – Méthode avec trisections		haut
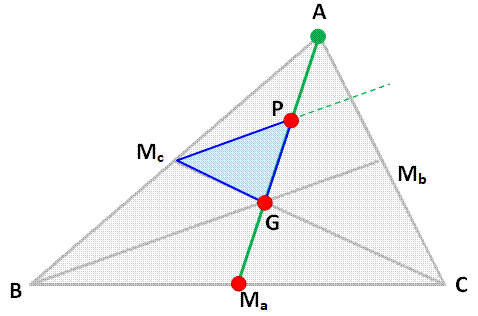
1. Construire le segment AMa. 2. Trisection de ce segment: points P et G. 3. Construire le triangle PGMc avec: GMc = 1/3 CMc, PMc = 1/2 BG = 1/3 BMb. 4. B est le symétrique de A par rapport à Mc. 5. McG est prolongé tel que McC soit égal à la mesure spécifiée.
Variante 1. Construire le triangle vert avec pour côtés les longueurs des médianes. 2. Trisection des trois segments: G, P et Q. 3. C est le symétrique de G par rapport à P. 4. B est le symétrique de Q par rapport à G.

Haut de page

Retour	Triangles quelconques – Construction
Suite	Tracé d'un vrai triangle quelconque
Voir	Constructions – Index Triangles – Index
Sites	Apprendre à construire : constructions de triangles #10 – Serge Mehl Construction of a Triangle Given 3 Medians – Chris Hood
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Construc/Mediane.htm