Construction du triangle à partir des centres

Édition du: 25/01/2021

INDEX Triangles Constructions Géométrie	CONSTRUCTION – TRIANGLE
	Types de triangles	Constructions élémentaires des triangles			Quadrature
	*Constructions*	Orientation	LLL	AAA	LAL …
	*Constructions*	Général	hhh	bbb	Centres
	Résol. des triangles	Quelconque	mmm	MMM	Milieu

L: côté; A: Angle; h: hauteur; m: médiane; M: médiatrice; b: bissectrice

Construction des triangles

connaissant certains CENTRES

Construire le triangle connaissant un triplet de points dont un ou deux sommets et certains centres du triangle, parmi les quatre classiques: Centre O du cercle circonscrit, centre de gravité G, orthocentre H et centre du cercle inscrit I.

Sommaire de cette page

>>> Faisabilité

>>> Construction (A, G, H)

Débutants

Triangle

Glossaire

Triangle

Anglais: Triangle (location) construction problems

Faisabilité

haut

Cette page couvre la construction des triangles dont on connait un ou deux sommets et un ou plusieurs des quatre centres classiques du triangle.

Au total, trois points sont connus.

Liste des cas possibles selon la nomenclature Wernick.

La seule connaissance de trois centres ne permet pas la construction.

Constructibles

S	A	B	C	O	G	H	I
4	X	X			X
7	X	X				X
10	X	X					X
13	X			X	X
16	X			X		X
19	X			X			X
40	X				X	X
43	X				X		X
57	X					X	X

NON-constructibles

U	A	B	C	O	G	H	I
73				X	X		X
80				X		X	X
121					X	X	X

Autres

Les autres cas sont pathologiques. Ils imposent des contraintes et conduisent à une infinité de solutions semblables ou pas.

Par exemple (A, B, O): les cercles (O, OA) et (O, OB) sont généralement distincts. Sinon, avec un cercle de centre O passant par A et B, le point C est sur le cercle et il y a une infinité de solutions.

Construction (A, G, H) – Cas 40		haut
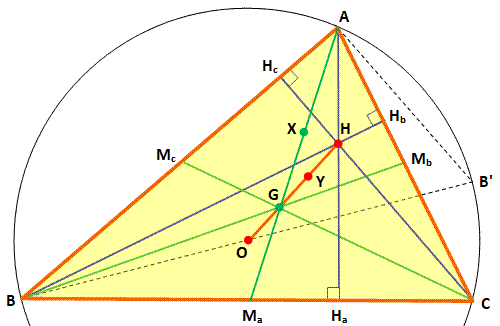
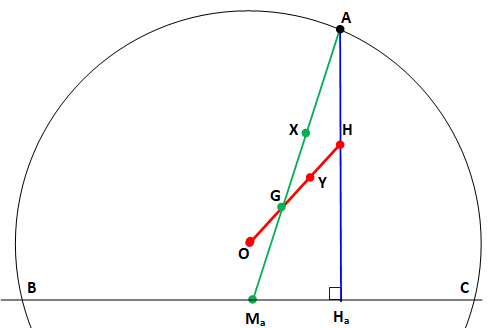
Problème Construire le triangle dont on connait la position: du sommet A, du centre de gravité G, et de l'orthocentre H. Propriétés L'astuce consiste à introduire le cercle circonscrit au triangle ABC. Si l'on connait son centre, on connait le lieu des points B et C. Or, dans tout triangle, les points H, G et O sont alignés (droite d'Euler). Et, de plus, G est au deux tiers du segment HO. On introduit le point Y comme point milieu de GH. La même propriété, plus connue, se retrouve sur la médiane, coupée au deux tiers par le centre de gravité. On introduit le point X comme point milieu de AG. Note: Le triangle ABB' est rectangle en A. Le segment BB' est un diamètre du cercle et O est son milieu.	Le sommet A est l'un des trois sommets du triangle à créer; Le point G est le point de concours des médianes; et, Le point H est le point de concours des hauteurs.
	AX = XG = GM_a HY = YG = G O
Construction 1. Demi-droites AG et AH 2. X milieu de AG 3. M_a symétrique de X par rapport à G. 4. Demi-droite HG 5. Y milieu de HG 6. O symétrique de Y par rapport à G. 7. Cercle (O, OA) 8. Perpendiculaire à AH passant par M_a. 9. Intersections B et C, les deux sommets cherchés.

Haut de page

Retour	Triangles quelconques – Construction
Suite	Construction à partir des médianes Tracé d'un vrai triangle quelconque
Voir	Constructions – Index Triangles – Index
Sites	Apprendre à construire : constructions de triangles #9 – Serge Mehl
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Construc/Centres.htm