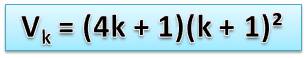|
Édition du: 22/07/2023 |
|
INDEX |
Cubes |
||
Faites un double-clic pour un retour en haut de page
![]()
|
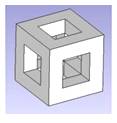
Volume du CUBE perforé
Un simple
cube perforé de part en part de trous carrés.
Quel est le volume du cube une fois évidé. Formule
pour k trous par côtés. Surprise, on retrouve la quantité de diviseurs du nombre
240. |
||
|
|
Sommaire de cette page >>> Le cube perforé 3x1 trous >>> Le cube perforé 3x4 trous >>> Le cube perforé 3x9 trous >>> Le cube perforé k trous par côté – Formule |
Débutants Glossaire |
|
Construction Un cube est percé de part en part par un trou
carré sur chaque face. Ces trous sont parfaitement localisés au milieu de
chaque face. Ils ont une section de 1 cm sur un cube de 3 cm de côté. Quelle est le volume du cube ainsi évidé ? Piste Ici, le dénombrement donne immédiatement le
volume du cube évidé. On cherche une solution applicable à un grand
nombre de trous. Raisonnement La foreuse perce le premier trou de part en part. Elle perce le second, mais rencontre un cube
central vide. Idem pour le troisième. |
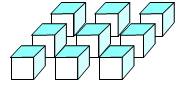
Cube à 3 perforations
Dénombrement On compte simplement les cubes présents:
Total: 20 |
|
|
Calculs
|
||
Voir Brève
52-1028
|
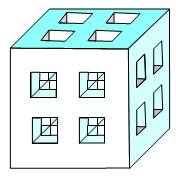
Construction Un cube est percé de part en part par quatre
trous carrés sur chaque face. Ces trous sont parfaitement localisés au milieu
de chaque quadrant. Ils ont une section de 1 cm sur un cube de 5 cm de côté. Quelle est le volume du cube ainsi évidé ? Piste La foreuse perce 3 x 4 trous. Cependant si le
premier perçage est complet, les deux suivants trouvent du vide aux intersections.
Il s'agit de quatre trous à deux niveaux: soit 4 trous x 2 niveaux x 2
directions = 16. |
Cube à 12 perforations
|
||
|
Calculs
|
|||
|
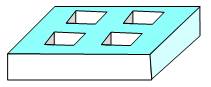
Solution alternative On découpe par la pensée le cube en cinq
tranches horizontales. Le volume vaut (voir ci-contre):
|
Les tranches 1, 3, 5 sont identiques
Les tranches 2 et 4 sont identiques
|
||
|
Construction Un cube est percé de part en part par neuf trous
carrés sur chaque face. Ces trous sont parfaitement localisés au milieu de
chaque tiers de face. Ils ont une section de 1 cm sur un cube de 7 cm de
côté. Quelle est le volume du cube ainsi évidé ? Piste La foreuse perce 3 x 9 trous de 7 cm. Au-delà du perçage
de la première face, pour les deux autres, chaque perçage rencontre 9 + 9 + 9
cubes déjà évidés. Volume V = 73 – 3 × (9×7) + 2 × (3×9) = 343 – 189 + 54 = 208 |
Cube à 27 perforations
Non à l'échelle ! |
|
|
Établissement de la formule de
calcul Si k est la quantité de perforations par côté,
soit k² par face. Le côté du carré vaut alors 2k + 1. Le volume du cube est (2k + 1)3. La quantité de perforations de part en part
devient: 3 × k² (2k + 1). La quantité de cubes vides rencontrés durant les perforations
des deux faces après la première est égale à: 2 × k3. Le volume du cube évidé devient:
Autre manière de voir Soit une simple grille cubique de taille (2n+1). Numéroter les coordonnées le long de chaque axe
de 1 à (2n+1). Sélectionnez uniquement les cellules qui ont au
moins deux coordonnées impaires et élimer le reste. Le nombre de cellules sélectionnées est le nombre
Vn. |
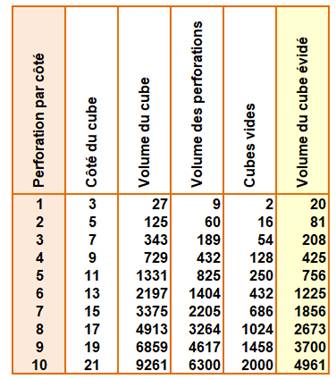
Table
|
||
|
Liste des nombres cubes évidés Vn |
1, 20, 81, 208, 425, 756, 1225, 1856, 2673, 3700, 4961,
6480, 8281, 10388, 12825, 15616, 18785, 22356, 26353, 30800, 35721, 41140,
47081, 53568, 60625, 68276, 76545, 85456, 95033, 105300, 116281, 128000,
140481, 153748, 167825, 182736, … OEIS A103532 |
||
|
Nombres cubes évidés et diviseurs Curieusement la suite des ces nombres est aussi
celle de la quantité de
diviseurs de 240n. On retrouve la formule La factorisation de 240 est en (4 + 1) (1 + 1) (1 + 1). Celle de 240² est en (8
+ 1) (2 + 1) (2
+ 1) Et sa puissance k en (4k
+ 1) (k + 1) (k
+ 1) |
Exemple Diviseurs (240):
{1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240}.
Quantité: 20. Aussi, avec sa factorisation:
|
||
Haut de page (ou
double-clic)
![]()
|
Retour |
||
|
Suite |
|
|
|
Voir |
||
|
Cette page |
||