NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 11/10/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Géométrie dans l'espace
Débutants Géométrie	Bases				Glossaire Géométrie
INDEX Géométrie		Plan	Perpendiculaires	Trois perpendiculaires
			Orthogonalité
		Sommaire de cette page >>> Approche >>> Définition >>> Vocabulaire >>> En pratique

ORTHOGONALITÉ

Différences entre

orthogonal,

perpendiculaire ou encore,

normal ?

Attention, ça coupe!

En bref

Perpendiculaire	Orthogonal
Spécifique aux droites sécantes, donc dans le plan.	Général: plan, vecteur, droites dans l'espace et dans le plan.
Une droite est perpendiculaire à une autre si et seulement si les deux droites sont sécantes en un point et que l'angle entre elles est de 90°.	Dire que deux droites de l'espace sont orthogonales signifie qu'une parallèle de l'une des droites est perpendiculaire à l'autre.

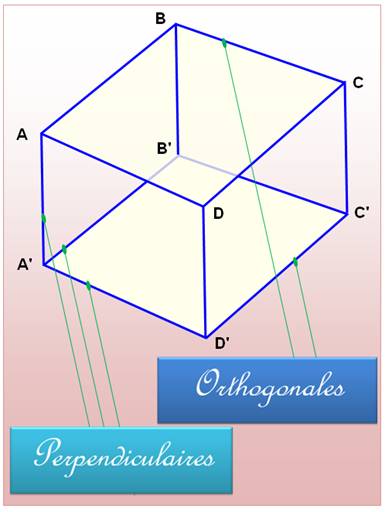
Autre subtilité: on dit: droites sécantes ou droites qui se coupent ou droites qui ont un point commun. Dans le cas de segments, comme les côtés d'un cube, on utilise aussi ces expressions en sous-entendant: "les droites qui portent ces segments".

Anglais: tantamount (to be – to) = équivalent (être – à)

Approche – Maître-mot: intersection ou non!
Prenons un cube. Il est formé par deux jeux de quatre arêtes parallèles. Nous savons que trois arêtes réunies par le même sommet sont perpendiculaires: elles se coupent à angle droit. Que dire des arêtes BC et C'D'? Elles ne sont pas parallèles. Elles ne se coupent pas. Elles ressemblent à des droites perpendiculaires mais à distance. Elles sont orthogonales. La notion d'orthogonalité est une généralisation de la perpendicularité. BC et C'D' sont orthogonales car on peut trouver B'C', une parallèle à BC, qui coupe C'D' à angle droit. A'A, A'B' et A'D' sont des segments orthogonaux qui se coupent, ils sont perpendiculaires.

ORTHOGONAL – Définition
Deux droites D et D' portant les segments AB et CD. Ces droites sont quelconques (pas coplanaires). En un point M quelconque, on trace les segments A'B' et C'D' (verts) parallèles à AB et CD. S'ils se coupent à angles droit, les droites D et D' sont orthogonales. Bien sûr, il est possible de choisir le point M sur une des droites et de tracer la parallèle à l'autre droite. Exemple avec N sur D' et le segment parallèle A"B" (rouge). 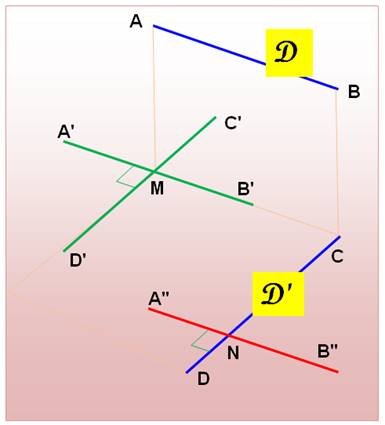Dire que deux droites de l'espace sont orthogonales signifie que: il est possible de tracer une parallèle à l'une des droites qui est perpendiculaire à l'autre.

ORTHOGONAL – Subtilités du vocabulaire
Espace	Deux droites sont orthogonales si elles sont parallèles à des droites se coupant en angle droit. Une droite orthogonale à toutes les droites du plan est orthogonale (on dit aussi perpendiculaire ou normale) au plan. Il suffit qu'elle soit orthogonale à deux droites sécantes de ce plan.

Plan	Deux droites orthogonales et sécantes sont perpendiculaires. Elles forment nécessairement un plan.
Perpendiculaire	S'applique aux droites dans le plan qui se coupent à angle droit (géométrie 2D).
Orthogonal	S'applique à l'espace: généralisation de la perpendicularité en 3D (sans obligation d'intersection); s'applique aussi aux vecteurs.
Normalité	S'applique à une droite ou un vecteur par rapport à un plan. Droite normale à un plan: droite qui est perpendiculaire à deux droites distinctes de ce plan. Avec un vecteur, implique souvent que le vecteur est unitaire.

2 vecteurs	Sont orthogonaux (on ne dit pas perpendiculaires).
2 droites	Sont orthogonales si leurs vecteurs directeurs sont orthogonaux. Sont perpendiculaires si orthogonales et sécantes. Dans un plan, deux droites non parallèles sont toujours sécantes. Si elles se coupent en formant un angle droit (donc quatre angles droits), elles sont perpendiculaires. Les directions des droites sont orthogonales et les droites (qui portent les segments) sont aussi orthogonales.
2 segments	Deux segments peuvent être orthogonaux s'ils ont des directions orthogonales. Deux segments peuvent être perpendiculaires s'ils se coupent à angle droit.
1 droite et 1 plan	Ils sont orthogonaux ou perpendiculaires.
1 vecteur et 1 plan	Le vecteur est normal au plan.
2 cercles	Les tangentes aux points d'intersection sont orthogonales >>>

ORTHOGONAL – Cas pratiques
Deux droites parallèle D et D'. Toute droite orthogonale à l'une l'est aussi pour l'autre. Tout plan orthogonal à l'une est orthogonal à l'autre.	Si deux plans sont parallèles, toute droite orthogonale à l'un est orthogonale à l'autre.

Deux droites orthogonales ne sont pas généralement pas perpendiculaires. Une droite est orthogonale à un plan si elle est orthogonale à deux droites sécantes (cad. non parallèles) du plan. Elle est alors orthogonale à toutes les droites du plan. Deux plans orthogonaux à une même droite sont parallèles. Si deux droites sont parallèles, tout plan orthogonal à l'une est orthogonal à l'autre. Voir Démonstration

Deux droites perpendiculaires sont aussi orthogonales. Deux droites orthogonales à une même troisième ne sont pas nécessairement parallèles. Elles le deviennent si les deux droites sont dans le même plan. Deux droites orthogonales à un même plan sont parallèles. Si une droite est orthogonale à deux plans, alors des deux plans sont parallèles.

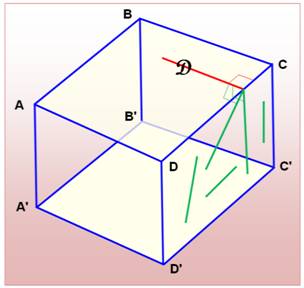
Un plan P' est perpendiculaire à P s'il existe une droite de Q orthogonale à P. Les faces non-parallèles du cube sont orthogonales. La droite D est orthogonale à toutes les droites vertes. Si P Q et P' Q alors P et P' ne sont pas nécessairement parallèles. Avec le cube les faces sont mêmes orthogonales par trois. Deux plans Q et Q' qui se coupent en D. Si ces deux plans sont perpendiculaires à un plan P, alors D est orthogonale à P.

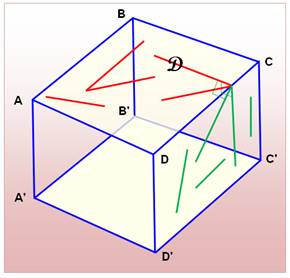
Les plans P et P' sont orthogonaux. Toute droite de P' n'est généralement pas orthogonale à toute droite de P. Les droites en rouge ne sont pas, en général, orthogonales aux droites en vert. Exemple typique: deux droites partant d'un point d'une arête et, se rapprochant de cette arête forment un angle très aigu. Pour visualiser: posez un crayon sur votre bureau avec une extrémité en bordure. Tenez l'autre pendant à l'extrémité du premier. Faites pivoter ce dernier dans le plan vertical.

Suite	Théorème des trois perpendiculaires
Aussi	Cristaux Cube Cube de Rupert Cubes (nombre au) Cubes et carrés Géométrie – Index Vocabulaire de la géométrie
Cette page	http://villemin.gerard.free.fr/GeomLAV/Objet3D/Orthogon.htm