NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/09/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	Propriétés			Glossaire Géométrie
INDEX Cercle Géométrie	Propriétés	Équations	Théorèmes
	Fondements	Angles	Partage
	Sécante	Tangente	Sécantes et tangentes
	Tangentes et corde soulevée		Arcs, cordes et sagittas
	Cordes parallèles et rayon du cercle
		Sommaire de cette page >>> Théorème des angles alternés >>> Exemples >>> Deux cercles et sécantes >>> Le triangle isocèle

Cercle: sécantes et tangentes

Cas de triangles inscrits dans un cercle et des tangentes aux sommets.

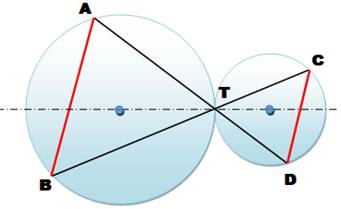
Théorème des angles alternés et applications; Découverte d'une bine belle propriété relative à deux cercles tangents et à deux sécantes.

Théorème des angles alternés
Théorème Un cercle et une tangente. Un triangle inscrit dans le cercle. Aux sommets, les angles avec la tangente sont égaux aux angles alternés du triangle. Explication Les angles interceptent les mêmes arcs. Or, les angles inscrits interceptant le même arc sont égaux.
Avec ce genre de figure, le même angle se retrouve trois fois. Démonstration Dessiner les trois rayons vers les sommets du triangle qui créent trois triangles isocèles. Ces rayons sont perpendiculaires aux tangentes. Il suffit alors d'évaluer les angles. En effet: A = x + y B = 90° – z Autour du centre: (180 – 2x) + (180 – 2y) + (180 – 2z) = 360° 2x + 2y + 2z = 180° x + y = 90 – z => A = B

Anglais: alternate segment theorem or tangent-chord theorem

Voir Brève 53-1043

Exemples
L'angle au centre (100°) vaut deux fois l'angle inscrit (50°).	Les deux angles le long de la tangente déterminent la valeur des deux autres angles du triangle.
Cercle et deux tangentes à 30°. Les deux tangentes forment un triangle isocèle avec angles à la base de 75° = (180 – 30) / 2. L'angle opposé vaut 75° quelle que soit la position du sommet sur le cercle.

Deux cercles tangents et droites sécantes
Problème Deux cercles tangents en T. Deux sécantes passant par T et coupant les cercles en A, B, C et D. Montrer que les droites passant par AB et CD sont parallèles. Solution (figure du bas) On trace la tangente commune en A (verte) et la solution devient évidente. Application du théorème des angles alternés dans chacun des cercles (interception du même arc): les angles marques 1 sont égaux (arc AT); les angles marques 2 sont égaux (arc TD). Or, les angles 1 et 2 en T sont égaux. L'angle en B est égal à l'angle en C. Même chose pour l'angle en A qui est égal à l'angle en D. Les deux triangles sont semblables et les troisièmes côtés, AB et CD, sont parallèles.
Problème Deux cercles tangents. Une droite tangente aux deux cercles. Le triangle ABT avec les points de tangence pour sommets. Quelle est la valeur de l'angle ATB ? Solution Les segments de tangente à un cercle, issue d'un même point, sont égaux. (isométriques). MA = MT = MB Si M est le centre d'un cercle de rayon MA, alors B et T sont sur ce cercle. AB est le diamètre et le triangle ABT, inscrit dans le demi-cercle, est rectangle en T.

Voir Brève 687

Le triangle isocèle
Problème Un cercle bleu. Un triangle BCE. Les deux tangentes en B et C et leur intersection en D. La parallèle DF à BE. Montre que le triangle BEF est isocèle. Solution (figure du bas) Les angles marqués 1 sont égaux selon ce qui a été vu ci-dessus. Avec les parallèles: les angles marqués 2 sont alaternes-internes et sont égaux. l'angle 3 est égal à l'angle 1 en E. L'angle 1 en B intercepté CD. L'angle 3 en F intercepté CD. CD est la corde commune d'un cercle. Les points BFCD sont cocyclique (cercle en pointillé). Dans ce cercle: l'angle 1 en C intercepte l'arc BD l'angle 2 en F intercepte l'arc BD Ils sont égaux. Les angles marqués 1, 2 et 3 sont tous égaux. En particulier, l'angle 2 en B et l'angle 1 en F. Le triangle BEF est isocèle et FB = FE.

Suite	Équations Fondements
Voir	Cercle – Index Géométrie – Index
Sites	Alternate Segment Theorem – Cuemath Alternate Segment Theorem – Explanation & Examples – The Sory of Mathematics
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/SecTang.htm