|
Édition du: 04/01/2025 |
|
INDEX |
Carrés – Motifs |
||
![]()
|
CARRÉS = Carré × Carré Il existe une grande variété de motifs faisant intervenir la
concaténation et les carrés. Ces pages
en présentent plusieurs types:
Il n'existe pas de noms avérés, en français comme en
anglais, pour ces variétés de nombres. |
||||||||
|
|
Sommaire de cette page >>> Carré = Carré × Carré >>> Carré = Carré × Carré / Records >>> Hautement composés |
Débutants Glossaire |
||||||
Anglais: Concatenated squares
|
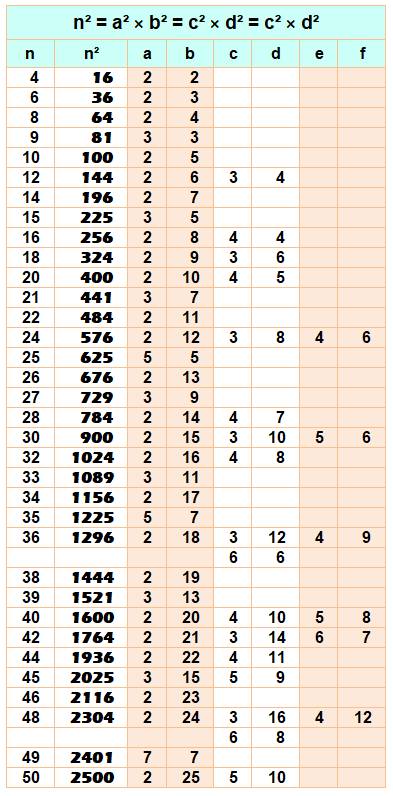
Tableau des
nombres de 1 à 50 dont le carré est égal au produit de deux carrés, une fois
ou plusieurs fois Une fois 36 = 6²
= 2² × 3² = 4 × 9 Deux fois 144 = 12²
= 2² × 6² Trois fois 576 = 24²
= 2² × 12²
= 4² × 6² Quatre fois 2304 = 48²
= 2² × 24²
= 4² × 12² |
|
|
|
Quantité record de motifs pour n jusqu'à 2 500. 2520²
est vingt-trois fois produits de deux carrés. Le
nombre 1516237305382800² semble être le record ultime avec 1 439 produits.
(?) |
k, n,
n² , [ [a, b], [ …] ] 1,
4, 16, [[2, 2]] 2,
12, 144, [[2, 6], [3, 4]] 3,
24, 576, [[2, 12], [3, 8], [4, 6]] 4,
36, 1296, [[2, 18], [3, 12], [4, 9], [6, 6]] 5,
60, 3600, [[2, 30], [3, 20], [4, 15], [5, 12], [6, 10]] 7,
120, 14400, [[2, 60], [3, 40], [4, 30], [5, 24], [6, 20], [8, 15], [10, 12]] 8,
180, 32400, [[2, 90], [3, 60], [4, 45], [5, 36], [6, 30], [9, 20], [10, 18],
[12, 15]] 9,
240, 57600, [[2, 120], [3, 80], [4, 60], [5, 48], [6, 40], [8, 30], [10, 24],
[12, 20], [15, 16]] 11,
360, 129600, [[2, 180], [3, 120], [4, 90], [5, 72], [6, 60], [8, 45], [9,
40], [10, 36], [12, 30], [15, 24], [18, 20]] 14,
720, 518400, [[2, 360], [3, 240], [4, 180], [5, 144], [6, 120], [8, 90], [9,
80], [10, 72], [12, 60], [15, 48], [16, 45], [18, 40], [20, 36], [24, 30]] 15,
840, 705600, [[2, 420], [3, 280], [4, 210], [5, 168], [6, 140], [7, 120], [8,
105], [10, 84], [12, 70], [14, 60], [15, 56], [20, 42], [21, 40], [24, 35],
[28, 30]] 17,
1260, 1587600, [[2, 630], [3, 420], [4, 315], [5, 252], [6, 210], [7, 180],
[9, 140], [10, 126], [12, 105], [14, 90], [15, 84], [18, 70], [20, 63], [21,
60], [28, 45], [30, 42], [35, 36]] 19,
1680, 2822400, [[2, 840], [3, 560], [4, 420], [5, 336], [6, 280], [7, 240],
[8, 210], [10, 168], [12, 140], [14, 120], [15, 112], [16, 105], [20, 84],
[21, 80], [24, 70], [28, 60], [30, 56], [35, 48], [40, 42]] 23,
2520, 6350400, [[2, 1260], [3, 840], [4, 630], [5, 504], [6, 420], [7, 360],
[8, 315], [9, 280], [10, 252], [12, 210], [14, 180], [15, 168], [18, 140],
[20, 126], [21, 120], [24, 105], [28, 90], [30, 84], [35, 72], [36, 70], [40,
63], [42, 60], [45, 56]] |
|
Voir DicoNombre 24 / 36 / 48 / 360
|
Suite des records La suite des nombres record (n) est
en fait la suite des nombres hautement composés k (k>6) qui restent
hautement composés lorsqu'ils sont divisés récursivement par un nombre sans
carré. Liste 1, 2, 4, 6, 12, 24,
36, 60, 120, 180, 360, 720, 840, 1260, 2520, 5040, 7560, 25200, 27720, 55440,
83160, 277200, 720720, 1081080, 3603600, 10810800, 21621600, 61261200,
183783600, 367567200, 3491888400, 6983776800, 48886437600, 73329656400,
80313433200, 160626866400, 1124388064800, 1686582097200, 32607253879200,
48910880818800, 1010824870255200, 1516237305382800 |
Exemples 1
est dans cette séquence puisque f(1) = 1 et 1 est hautement composé. 2
est dans cette séquence puisque f(2) = 1 et 1 est hautement composé. 12
est dans cette séquence puisque f(12) = 2 et f(2) = 1, tous deux hautement
composés. 48
n'est pas dans cette séquence puisque f(48) = 48/6 = 8 et 8 n'est pas
hautement composé. L'application
récursive de f à h(128) = 1516237305382800 donne la chaîne suivante : 1516237305382800 = 1,51 …
1015 |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |