|
Édition du: 24/05/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||
|
36 = 2 (3.6) |
|||
|
Caractérisation
du nombre
|
|
Voir |
|
![]()
Propriétés MATHÉMATIQUES
Chiffres et numération
|
36
= 3! x 6 |
|
|||
|
36
+ 63 = 99 63
– 36 = 27 = 33 |
|
|||
|
36 =
3+6 + 4+6+6+5+6 363
= 46 656 |
Somme de ses chiffres et de ceux de son
cube. |
|||
|
3610 = 1215 = 448 =
3311 =2217 |
|
|||
|
36 =
3311 = 3! x 3! = 3.11 + 3 |
|
|||
|
|
Voir Nombre 18 |
|||
|
3
x 6 = 2 (3 + 6) |
Liste:
36, 44, 63, 138, 145, 154, 183, 224, 242, 318, 381, 415, 422, 451, 514, 541,
813, 831 |
||
|
36 =
6² &
3 + 6 = 9 = 3² |
|
||
|
36²
= 1 296 36 =
(3x6) + (1+2+9+6) |
|
||
|
36 =
6 x 6 |
|
||
|
12 =
4 x (1 + 2) & 21 = 7 x (2 + 1) 24 = 4 x (2 + 4) & 42 = 7 x (4 + 2) 36 = 4 x (3
+ 6) & 63 = 7 x (6 + 3) 48 = 4 x (4 + 8) & 84 = 7 x (8 + 4) |
|
||
|
|
|
||
|
36 =
9 x 4 = 18
x 2 |
|
||
Vincent Elbaz – Acteur français né en 1971
|
Ce nom
d'artiste se prête à une interprétation en chiffres dont la valeur varie
selon la base utilisée 20 100 et les bases
(Vincent Elbaz) est un allographe, et
2010010 se décline en divers nombres selon les bases. En binaire:
20 1002 => 2x24 + 0x23 + 1x22
+ 0x21 +2x20 = 32 + 0 + 4 + 0 + 0 = 3610 . En ternaire:
20 1003 => 2x34 + 0x33 + 1x32
+ 0x31 +2x30 = 2x81 + 9 = 17110 Pour les bases de 2 à
16:
|
Addition et soustraction
|
36 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 1 + 3 + 5 + 7 + 2 + 4 + 6 + 8 |
Les nombres
triangulaires et carrés sont rares: 1, 36, 1225, 41616, 1413721, 48024900,
1631432881, … OEIS A001110
|
|
|
36
= 1 + 3 + 5 + … + 11 = 6² = 1 + 12 + 23 |
|
|
|
36
= 1 + 3 + 5 + 7 + 9 + 11 36
= 17 + 19 |
|
|
|
36
= 17 + 19 36/2
– 1 = 17 |
Liste: 36, 144, 1764, 2304, 5184, 7056, 8100, 30276,
41616, 69696, 93636, 138384, 166464, … |
|
|
36
= 17 + 19 = 5 + 7 + 11 + 13 |
Plus petit nombre dans ce cas. |
|
|
36 =
1 + 2 + 3 + 4 |
|
|
|
36
= 3 + 33 |
|
|
|
36 =
T8 = T5 + T6 = 15 + 21 |
|
|
|
36 +
35 + 35 + … + 2 + 1 = 36 x 37 / 2 = 666 |
|
|
|
36 3+6 =
9 => 9² = 81 & 3x6 = 18 |
|
|
|
36
= 6² = 1 + 3 + 5 + 7 + 9 + 11 |
|
|
|
36
+ 37 + … + 42 =
43 + … + 48 |
|
|
|
36
= (9+1) + (9-1) + (9x1) + (9/1) = (8+2) + (8-2) + (8x2) + (8/2) = (5+5) + (5-5) + (5x5) + (5/5) |
|
|
Multiplication, division, diviseurs
|
|
Liste: 36,
40, 72, 96, … OEIS A334911 Objet de
la célèbre énigme des trois filles. |
|
|
36 / (3 + 6) = 4 |
|
|
|
36
= 6 x 6 = 6² |
|
|
|
36
= 4 x 9 = 2 x 2 x 3 x 3 = 2² x 3² |
|
|
|
36
= 2 x 18 = 2 (3 x 6) |
|
|
|
|
|
|
|
|
|
|
|
36
= 3 x 3 x 2 x 2 10
= 3 + 3 + 2 + 2 |
|
|
|
36
= 22 . 32 |
||
|
2 x
18 = 36 3 x
12 = 36 4 x 9 = 36 6 x 6 = 36 |
|
|
|
36 = 6² 36 = 6 x 6 36
= 3! x 6 |
|
|
|
36 =
6² = 4 x 9 = 2² x 3² |
|
|
|
36 = 6, 12, 18 = … =
2, 3, 4, 6, 9, 12 |
|
|
|
Somme des diviseurs propres = 55 |
36 est la somme des diviseurs de 24, |
|
|
36
a 9 diviseurs |
|
|
|
36
= tau (1 260) |
|
|
|
D(36) = 1, 2, 3, 4, 6, 9, 12, 18, 36 |
|
|
Avec les puissances
|
36 =
6² 3 + 6 = 9 = 3² |
|
||||||||||||||
|
36 =
6² =
2² + 4² + 4² =
1² + 1² + 3² + 5² =
3² + 3² + 3² + 3² =
1² + 1² + 3² + 3² + 4² |
|
||||||||||||||
|
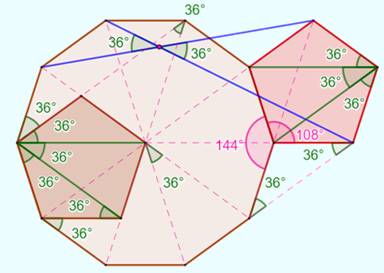
Jolis motifs avec des carrés et des cubes
|
|||||||||||||||
|
36
= 4 x 12 + 8
x 22 = 4 x 13
+ 4 x 23 = 7 x 22
+ 8 x 12 = 1 x 22
+ 8 x 22 = 2 x 22
+ 7 x 22 = 3 x 22
+ 6 x 22 = 4 x 22
+ 5 x 22 = 1 x 22
+ 2 x 42 = 4 x 13
+ 4 x 13 |
= 3 x 32
+ 9 x 12 = 1 x 32
+ 3 x 32 = 2 x 32
+ 2 x 32 = 2 x 24
+ 4 x 14 = 2 x 42
+ 4 x 12 = 1 x 42
+ 5 x 22 = 1 x 33
+ 9 x 13 = 1 x 25
+ 4 x 15 |
|
|||||||||||||
|
36 =
6² = 2² + 4² + 4² = 2² (1 + 23) = 1² + 1² + 3² + 5² = 3² + 3² + 3 ² + 3² = 4 . 3² = 13 + 23 + 33
= 15 + 15 + 15
+ 15 + 25 |
|
||||||||||||||
|
36
= (3² + 3²)(1² + 1²) = (6² + 0²) = 3² + 3² + 3² + 3² |
|||||||||||||||
|
13 + 23 + 33 = 6 x 6 = 36 36 = (1×1)3 + (2×1)3 + (3×1)3 |
Voir même propriété pour le Nombre
204 |
||||||||||||||
|
36 =
21 + 32 + 52 = 22 + 33
+ 51 = 23 + 31
+ 52 |
|
|
36
= 53 – 2x63
+ 73 = 6 x 6
|
|
|
36
= 82 – 72 + 62
– 52 + 42 – 32 + 22 – 12 |
|
|
36
= 11 + 21 + 31 + 41 + 51
= 4 x 9 |
|
|
36
= (1 + 2 + 3)² |
|
|
36
= 3² + 3² + 3² + 3² |
|
|
36
= 13 + 23 + 33 = (1 + 2 + 3)² |
Voir Autour de 12345 |
|
36
= 13 + 23 + 33 = 9 x 4 |
|
|
36
= 2 2 + 2 5 = 6 2 36
= 3 2 + 3 3 = 6 2 |
|
|
36
= 10² – 8² = 6² |
|
|
–36 = ( |
|
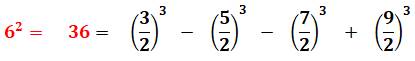
Identité
impliquant quatre nombres impairs successifs
Voir Brève 61-1218 / Nombre 6 en puissances
|
|
|
|
236 =
68719476736 2736
= … 736 28736
= … 8736 248736
= … 48736 … |
|
|
36² = 1 296 |
|
|
363
= 46 656 |
|
|
364 = 1
679 616 & 1+6+7+9+6+1+6 = 36 365 = 60
466 176
& 6+0+…+7+6 = 36 |
|
|
3610 = 3 656 158 440 062 976 |
|
Dénombrement, jeux et curiosités
|
36
= 3! × 3! = 3! + 3! + 4 ! |
|
|
|
36
= 6 x 6 = 6² |
|
|
|
|
|
|
|
36 pour {12, 13, 14, 15,
16, 17, 18, 19, 23, 24, 25, 26…} |
|
|
|
36 |
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20,
21, 24, 25, 27, 28, 30, 32, 35, 36, 40, 42, 45, 48, 49, 54, 56, 63, 64, 72,
81. |
|
|
36 |
|
|
|
9,
10, 17 3,
25, 26 |
|
|
|
36
nombres
"consécutifs" |
|
|
|
36
segments
avec un cube |
|
|
|
|
|
|
Autour du nombre
|
1
/ 36 = 0, 0277... |
|
|
|
36° = |
|
|
|
base 36 |
Dans cette base, tous les mots
sont des nombres. |
|
Décimales
|
36,8 % |
|
|
36,86989765 …° |
|
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2, [1, 0, 0, 1, 0, 0] 3, [1, 1, 0, 0] 4,
[2, 1, 0] 5, [1, 2, 1] 6,
[1, 0, 0] 7,
[5, 1] 8, [4, 4] |
9,
[4, 0] 10,
[3, 6] 11, [3, 3] 12,
[3, 0] 13,
[2, 10] 14,
[2, 8] |
15,
[2, 6] 16,
[2, 4] 17, [2, 2] 18,
[2, 0] 19,
[1, 17] 20,
[1, 16] |
8,
[4, 4] 11,
[3, 3] 17,
[2, 2] 35,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite Retour |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()