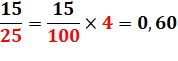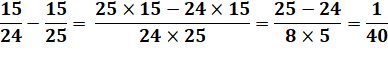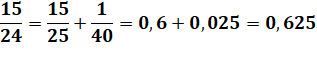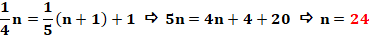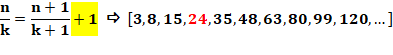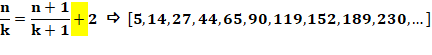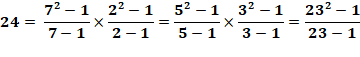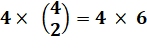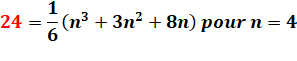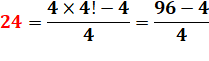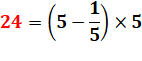|
Édition du: 05/05/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
|
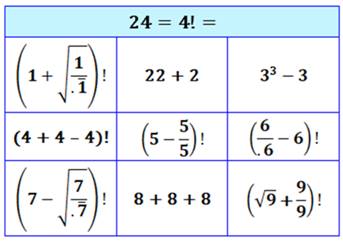
Maths générales du
24 |
Maths détaillées du 24 |
||
|
|
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||
|
24 = 1 × 2 × 3 ×
4 = 4! Nombre abondant non égal à la
somme de ses diviseurs abondants. Ce sont tous les nombres abondants dont
d'autres diviseurs sont abondants. |
|||
|
Caractérisation
du nombre
|
|
Voir |
|
Rappel Propriétés générales >>>
Faire 24 avec quatre nombres et les quatre
opérations
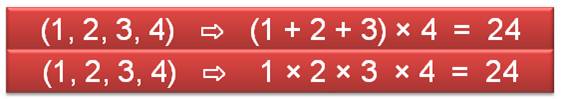
Voir Jeu
avec 24
Caractéristiques – Numération – Chiffres
|
24 =
(2 + 4) × 4 24 =
(2 × 4) × 3 |
|
||
|
24 = 4 + 4 + 4 × 4 |
|
||
|
24
= 2 + 4 + 5 + 7 + 6 242
= 576 24
= 2 + 4 + 1 + 3 + 8 + 2 + 4 243
= 13 824 |
Somme de ses chiffres et de ceux de son
carré. |
||
|
24 +
42 = 66 = T11 |
|
||
|
24 = |
|||
|
24 divisible
par 6 et 8 |
|
||
|
24 = 445 = 337 = 2211 = 1123 24 = 52 – 1 = (5 – 1)(5 + 1) = 4 x 115 |
|
||
|
24 + 3 = 27 24 x 3 = 72 |
|
||
|
624 + 15 = 639 624 x 15 = 9360 |
|
||
|
12 =
4 x (1 + 2) & 21 = 7 x (2 + 1) 24 = 4 x (2
+ 4) & 42 = 7 x (4 + 2) 36 = 4 x (3 + 6) & 63 = 7 x (6 + 3) 48 = 4 x (4 + 8) & 84 = 7 x (8 + 4) |
|
||
|
24 = 1 x 2 x 3 x 4 = 22 x 6 = 23 x 3 = 4! = 4 x 6 = 5! / 5 = 1x1x1x3x8 = 3!P |
|
||
|
24,
25, 26, 27, 28 |
|
||
|
|
|
||
|
24
= 2 x 3 x 4 |
|
||
|
24 = 2 (3 x 4) = 4 T3 = CC3
– 1 = 3² + 4²
– 1 7² + 24² = 25² 21² + 22²
+ 23² + 24² = 25² + 26² + 27² |
Ensemble
ces propriétés sont communes à toute une série de nombres: 4, 12, 24, 40 … |
||
|
24 =
406 = 4! x 0! = 4.6 + 0 |
|
||
![]()
Addition / Multiplication
|
p(24) = 1 575 |
|
||
|
|
C'est la quantité maximale de partitions
avec nombres distincts de 1 à 9.
|
||
|
24
= 7 + 8 + 9 |
|
||
|
24
= 11 + 13 |
|
||
|
24
= 2 + 22 |
|
||
|
24
= 1 + 8 + 15 |
|||
|
24 =
9 + 8 + 7 = 6 x 4 |
|
||
|
24
= (8 – 2) ( 8 – 4)
= 6 x 4 |
|
||
|
24
= (6+1) + (6-1) + (6x1) + (6/1) |
|||
|
1,
1, 2, 4, 7, 13, 24… |
Sommes successives des trois nombres
précédents. |
||
|
24
= 25 – 1 = 5² –
1 = 4 x 6 |
|
||
|
24 =
5² –
1 = 8 + 16 = 2 x 3 x 4 = 4 x 6 |
|
||
|
2 x
12 = 24 3 x 8 = 24 4 x 6 = 24 |
|
||
|
|
|
||
![]()
Calcul mental
|
Mon fils me demande: un paquet de
24 barres chocolatées vaut 15 euros. Quel est le prix d'une barre ? Voici trois réponses graduées en
complexité. |
|
|
1) Réponse
rapide Le calcul
mental de 15 divisé par 24 n'est pas facile. J'utilise le fait que 24 est proche de 25 et je divise par ce nombre:
En gros, la barre vaut un peu plus de 60 centimes. |
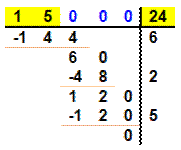
2) Bonus
simple Un raffinement, consiste à estimer l'erreur: 1 sur 25 = 4 sur 100 et 4% de 6 = 24. Je corrige avec cette valeur: Prix de la barre: 62,4 centimes. La valeur exacte est 62,5 comme le montre la division
posée:
|
|
3) Pour
les plus exigeants (toujours en utilisant 25)
|
|
Fractions de nombres consécutifs
|
Question: quel est le nombre n tel que son quart excède
le cinquième du nombre suivant d'une unité ? Réponse:
Généralisation: valeur de n selon k et supplément.
|
Nombre 24 et la division / divisibilité /
diviseurs
|
24 / (2 + 4) = 4 |
|
|
|
Facteurs(24): 2, 3 |
|
|
|
24 divisible par 2 + 4 et par 2 x 4 |
|
|
|
24 =
6 x 4 = 8
x 3 |
|
|
|
24 et nombres premiers |
|
|
|
PGCD(24,
2k+1 < 24) = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24
= |
||
|
24 =
|
|
|
|
24 = 4 + 8 + 12 = 1 + 3 + 8 + 12 = 2 +
4 + 6 + 12 = 1 + 2 + 3 + 6 + 12 = 1 + 2 + 3 + 4 + 6 + 8 |
|
|
|
Somme des diviseurs propres de 24
= 36 |
|
|
|
24 = 1 + 2 + 3 + 4 + 6 + 8 |
égal à la
somme certains de ses diviseurs. |
|
|
24 => {5, 7, 11, 13, 17, 19, 23} |
|
|
|
24
|
|
|
Suite Divisibilité
par 24
![]()
Puissance
|
24 =
3 x 23 |
|
|
|
24 et
bicarrés |
|
|
|
24 = 1 +
9 + 14 = 2
+ 7 +
15 = 1 + 9
+ 14 278 = 1² + 9² + 14² = 2² + 7² + 15² = 1² + 9² + 14² |
|
|
|
24 =
2² + 2² + 4² = 23 + 23 + 23 |
|
|
|
24
= 23 + 42 & 43 = 4²
+ 33 = 3 x 23 |
|
|
|
24
= 7² – 5 ² = 5² – 1² |
Sous deux formes 15 est le
plus petit ; le suivant est 21 Plus petite différence avec un écart de
4 ( = 5 - 1) |
|
|
1,
25, 49
|
|
|
|
21²
+ 22² + 23² + 24² = 25² + 26² + 27² = 2 030 |
|
|
|
24 = 25 –
23
= 33 – 31 |
|
|
|
24 = 210 – 103
= 45 – 103
= 322 – 103 |
||
|
24
= 33 – 2x43
+ 53 = 6 x 4
|
|
|
|
1²
+ 2² + 3² + … + 24² = 70² |
|
|
|
52 – 1 =
24 54 – 1 =
624 56 – 1 =
15624 58 – 1 = 390624 … |
|
|
|
p²
– 1 p²
– q² |
|
|
|
n
(n+1) (n+2) (n+3) |
|
|
![]()
En puissance
|
|
|
||
|
224 = 16 777 216 |
|
||
|
24² = 22 × 122
|
|
||
|
24² = 576 = 26
× 32 |
|
||
|
24²
= 43 + 83 = 64 + 512
= 576 |
Si
b = 2a alors b3 = 8a3 et c² = 9a3 Posons
c = 6a, alors 36a² = 9a3 En
simplifiant: 4 = a Méthode des anciens mathématiciens arabes. |
||
|
24²
+ 23² + …+ 1² = 1/6 (24 x
25 x 49) = 4 900 = 70² |
|
||
|
243 = 13824 |
|
||
|
243 = 123 + 163 + 203
= 43 (33 + 43 + 53) |
La
première résulte de la somme pour 63 La deuxième
est la seule somme avec trois ou quatre cubes distincts. |
||
|
24
et 42 48
et 84 |
|
|
|
24 =
22 + 2 = 33 – 3
|
|
|
|
24 = |
|
|
|
24
en
géométrie |
|
|
|
24
= 3 (14 – 6) = 13 x 4 x 6 = 6 / (1 – 3/4 ) |
La première, si la concaténation de deux
chiffres est permise (1 et 4 en 14). La deuxième, si les puissances sont
permises. La troisième est la seule et unique sans
puissance, ni concaténation. |
|
|
6, 8, 10 4,
13, 15 |
|
|
|
24!
= 620 448 401 733 239 439 360 000 |
|
|
|
|
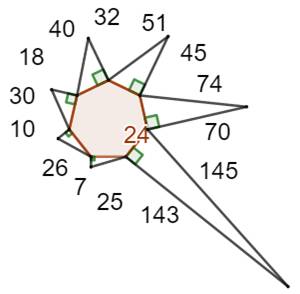
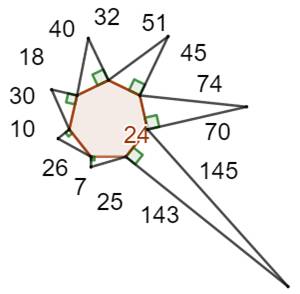
24² + 7² =
25² 24² + 10²
= 26² 24² + 18²
= 30² 24² + 32²
= 40² 24² + 45²
= 51² 24² + 70²
= 74² 24² + 143²
= 145² |
Décimales
|
1 / 24,5025 = 0,04 08 12 … |
|
|
24,97999199… = 25 – 0,020008 …
|
|
Dénombrement, jeux et curiosités avec 24
|
24 |
|
|||
|
24 |
|
|||
|
24 |
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
Voir Explication des notations en
nombre 1/3 Voir Nombre 4 Voir Jeux
semblables avec les chiffres |
|||
|
24 |
|
|||
|
Jeu du 24 |
|
|||
Solution: faire 24 avec trois "1"

|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2, [1, 1, 0, 0, 0] 3, [2, 2, 0] 4,
[1, 2, 0] 5, [4, 4] 6,
[4, 0] 7, [3, 3] 8,
[3, 0] |
9,
[2, 6] 10,
[2, 4] 11, [2, 2] 12,
[2, 0] 13,
[1, 11] 14,
[1, 10] |
15,
[1, 9] 16,
[1, 8] 17,
[1, 7] 18,
[1, 6] 19,
[1, 5] 20,
[1, 4] |
5,
[4, 4] 7,
[3, 3] 11,
[2, 2] 23,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Sites |
|
|
Cette
page |
![]()