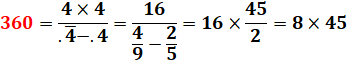Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 05/04/2025 M'écrire Brèves de Maths

Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 0,… / 1 / 10 / 50 / 100 / 200			300 à 399			400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100
	300	310	320		330	340		350	360	370	380	390
	360	361	362		363	364		365	366	367	368	369

Trois-cent-soixante

Three hundred sixty

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 0110 1000
Bases	[18, 18]19 FF23 CC29
Romain	CCC LX

Suite

Abondant

Abondant (hautement -)

Abondant (super -)

Abondant (colossalement -)

Brésilien (hautement: 11 fois)

Composé

Composé (hautement, 13^e)

Cunningham

Docile (amenable)

Fourchette ou gapful

Harshad

Pair

Pratique

Refactorisable ou tau

Semi-parfait

Sigma-touchable (hautement)

Zumkeller

Chiffres et numération

360 + (3 × 6) = 378 = T27	Devient triangulaire en lui ajoutant le produit de ses chiffres.
360 = 9939 = 8844 = … = 11359	Multi repdigit record avec 12 configurations, la dernière étant triviale => 11 fois brésilien.
360	Divisible par ses chiffres et par la combinaison de ses chiffres: 36, 30 et 60
		Les sept premiers multiples de 360 s'écrivent avec cinq chiffres romains. Seul cas avec 36.

Addition et soustraction

360 = 15 + 16 + … + 30	Une des cinq sommes de nombres consécutifs >>>
360 = 36 + 37 + … + 44 = 48 x 8	Somme de consécutifs, égale à un multiple du nombre suivant.
360 = 179 + 181	Somme de nombres premiers consécutifs.
360 = T3 + T4 + …+ T12	Somme de nombres triangulaires consécutifs.

Multiplication et division

360	Nombre semi-parfait: 22 208 fois somme de certains de ses diviseurs.
360 = 3 x 4 x 5 x 6 = 10 x 6²	Nombre Quadri Pronique. Produits de consécutifs multiples d'une puissance.
360 = 3 x 4 x 5 x 6 = 19² – 1 = 18 x 20	Produit de quatre nombres consécutifs. Propriété générale.
360 = 6! / 2 = 6! / (3 – 0!)	Moitié d'une factorielle. Opération avec les chiffres de 360.
360 est divisible par 2, 3, 4, 5, 6, 8, 9, 10 … = 2 x 6 x 30	Nombre hautement composé avec 24 diviseurs. Le précédent 240 en avait 20. Le suivant 720 en a 30. Divisible par tous les chiffres sauf 7 et même par 10. C'est le plus petit. Produit de trois primorielles.
(120, 174, 184, 190, 267, 295, 319, 323, 359)	Somme des diviseurs de neuf nombres. La plus petite. Record pour dix: n = 504.
360 = tau (3 603 600)	Quantité de diviseurs de 3 603 600, nombre hautement composé.

Avec les puissances

360 = 6² + 18²	Seule somme de deux carrés >>>
360 = 6² + 6² + 12² + 12²	Somme de carrés (exemple).
360 = 1^3 + 2^3 + 2^3 + 7^3 = 2^3 + 2^3 + 4^3 + 4^3 + 6^3	Sommes de cubes.

En puissance

360² = 129 600 = 4^2 × 90^2 = 5^2 × 72^2 = 6^2 × 60^2 = 8^2 × 45^2 = 9^2 × 40^2 = 10^2 × 36^2 = 12^2 × 30^2 = 15^2 × 24^2 = 18^2 × 20^2

Carré produit de deux carrés, neuf fois. Le plus petit cas.

Jeux

Jeu du quatre 4. Avec la notation anglaise: .4 = 0,4 = 2/5 et .4 surligné = 0,444… = 4/9

Culture

Voir Expressions en 360

Langue	Une vision 360: une vision panoramique. Utilisé pour indiquer l'appréciation d'une situation sur tous les plans.	>>>
Géométrie	360° Angle plein. Tour complet en degrés. Quantité de degrés pour le cercle. Idée de l'astronome grec Hipparque. Somme des angles d'un quadrilatère.	>>> >>>
	360 = 2^3. 3^2. 5 soit 24 diviseurs. Il existe 24-2 = 22 polygones réguliers dont les angles intérieurs sont des nombres entiers.	>>>
Construction	360° Immeuble au Brésil dont chacun des onze étages peuvent pivoter. De nombreuses villes possèdent une tour avec une partie pivotante au sommet, souvent dotée d'un restaurant donnant une vue panoramique de la ville. La duré d'un tour est voisine d'une heure en général. Existe notamment à Toronto (Canada), Sydney (Australie) … À Curitiba au Brésil un immeuble de 11 étages offre à chaque propriétaire un étage complet qui fait un tour en moins d'une heure, au prix d'amis de 226 k€ pour 300 m². En 2005, ce type d'immeuble est unique.	>>>
Géographie	0° ou 360° direction du NORD.	>>>
Social	360 sénateurs selon Platon	>>>
Calendrier	360 365 Approximation du nombre de jours dans une année.	>>>
Informatique	IBM System 360 (1964) Signifiant compatible sur les 360°, autrement-dit partout, sur tous les modèles de la gamme.	>>>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 0, 1, 1, 0, 1, 0, 0, 0] 3, [1, 1, 1, 1, 0, 0] 4, [1, 1, 2, 2, 0] 5, [2, 4, 2, 0] 6, [1, 4, 0, 0] 7, [1, 0, 2, 3] 8, [5, 5, 0] 9, [4, 4, 0] 10, [3, 6, 0] 11, [2, 10, 8]	12, [2, 6, 0] 13, [2, 1, 9] 14, [1, 11, 10] 15, [1, 9, 0] 16, [1, 6, 8] 17, [1, 4, 3] 18, [1, 2, 0] 19, [18, 18] 20, [18, 0] 21, [17, 3]	22, [16, 8] 23, [15, 15] 24, [15, 0] 25, [14, 10] 26, [13, 22] 27, [13, 9] 28, [12, 24] 29, [12, 12] 30, [12, 0] 60, [6, 0]	19, [18, 18] 23, [15, 15] 29, [12, 12] 35, [10, 10] 39, [9, 9] 44, [8, 8] 59, [6, 6] 71, [5, 5] 89, [4, 4] 119, [3, 3] 179, [2, 2] 359, [1, 1]

Voir Bases / Brésiliens

Retour Suite	Nombres en 350 Nombres en 370
Voir	Nom des nombres Nombres géométriques
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres

Cette page

http://villemin.gerard.free.fr/NombDico/N100a500/Nomb300/Nb360.htm