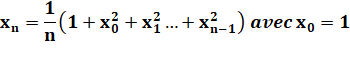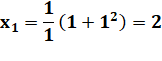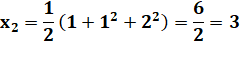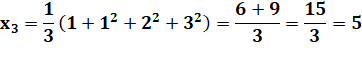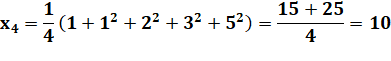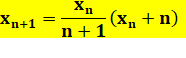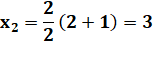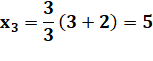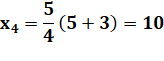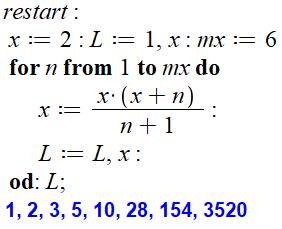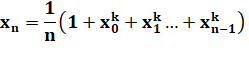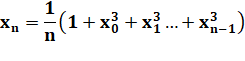suites de nombres, Göbel

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/05/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Suites & Séries
Débutants Général	CLASSIQUES				Glossaire Suites
INDEX Suites	Général		Harmonique	Suite aliquote
	Typiques		De Farey	Séquences numériques
			De Martin-Löf	Thue Morse
	Göbel		Engel	Kempner
		Sommaire de cette page >>> Suite de Göbel >>> Suite de Göbel généralisée >>> Entier ?

SUITE de GÖBEL

Les valeurs de cette suite récurrente sont souvent des entiers, mais pas toujours.

Avec la suite généralisée d'ordre k, il existe toujours au moins une valeur non entière pour chaque k.

Suite de Göbel (simple)
Suite
Exemple avec x₀ = 1
Formule de récurrence
Exemple avec x₁ = 2

Liste pour n de 0 à 9	1₀, 2₁, 3₂, 5₃, 10₄, 28₅, 154₆, 3520₇, 1551880₈, 267593772160₉,
Liste pour n jusqu'à 20. Croissance extrêmement rapide.		1, 2, 3, 5, 10, 28, 154, 3520, 1,551880 × 10^6, 2,675937722 × 10^11, 7,160642690 × 10^21, 4,661345794 × 10^42, 1,810678718 × 10^84, 2,521967245 × 10^167, 4,543084847 × 10^333, 1,375974662 × 10^666, 1,183316419 × 10^1331, 8,236692630 × 10^2660, 3,769061416 × 10^5320, 7,476749450 × 10^10639
Programme		But Lister les valeurs de la suite de Göbel. Programme Maple Initialisation des paramètres; notamment la suite L amorcée avec les valeurs 1, 1 et 2. Boucle de calcul en n en appliquant simplement la formule de récurrence. La suite L est complétée par la nouvelle valeur calculée. Notez que L est une suite (une sorte de tuple selon la terminologie Python) et non une liste.

Voir Programmation – Index / Traitement des suite, liste et ensembles

Suite de Göbel – Généralisée d'ordre k
Suite définie par récurrence
Cas du cube ou 3-Göbel	Liste: 1, 2, 5, 45, 22815, 2375152056927, …

Entier ?
La première valeur non entière pour l'ordre 2 (k = 2) est trouvée pour x(43)	Une valeur tellement grande (proche de 180 milliards de chiffres) que ce résultat a été trouvé par test de congruence.
La première valeur non entière pour l'ordre 3 (k = 3) est trouvée pour x(89)	Même remarque.
Quel que soit l'ordre, il existe au moins une valeur non entière. Liste des cas non-entiers pour k successifs à partir de 2.	43₂, 89₃, 97, 214, 19, 239, 37, 79, 83, 239, 31, 431, 19, 79, 23, 827, 43, 173, 31, 103, 94, 73, 19, 243, 141, 101, 53, 811, 47, 1077, 19, 251, 29, 311, 134, 71, 23, 86, 43, 47, 19, 419, 31, 191, 83, 337, 59, 1559, 19, 127, 109, 163, 67, 353, 83, 191, 83, 107, 19, 503, …

Suite	Voir en-tête pour autres suites
Voir	Séquences numériques Série 1 + 2x + 3x² + ... Suite d'Euclide-Mullin Suite de Kolakoski Suite de la copie augmentée Suite de l'artiste ou des 2/3 Suite harmonique déguisée Hofstadter–Conway Suite logistique Suite qui rend fou Suites fractales
Livre	Dictionnaire de (presque) tous les nombres entiers – Daniel Lignon – ellipse – 2012 – pages 397et 398
Sites	Göbel's sequence – Wikipedia Göbel's sequence – Wolfram MathWorld OEIS A003504 – a(0)=a(1)=1; thereafter a(n+1) = sum(a(k)^2,k=0..n)/n (a(n) is not always integral) OEIS A005166 – a(0) = 1; a(n) = (1 + a(0)^3 + ... + a(n-1)^3)/n (not always integral) OEIS A108394 – Least k for which f(k) = (1 + f(0)^n + f(1)^n + ... + f(k-1)^n)/k, f(0) = 1, is non integral
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Suite/Suite.htm

Suite	Voir en-tête pour autres suites
Voir	Séquences numériques Série 1 + 2x + 3x² + ... Suite d'Euclide-Mullin Suite de Kolakoski Suite de la copie augmentée Suite de l'artiste ou des 2/3 Suite harmonique déguisée Hofstadter–Conway Suite logistique Suite qui rend fou Suites fractales
Sites	Göbel's sequence – Wikipedia Göbel's sequence – Wolfram MathWorld OEIS A003504 - a(0)=a(1)=1; thereafter a(n+1) = sum(a(k)^2,k=0..n)/n (a(n) is not always integral!)
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Suite/Suite.htm