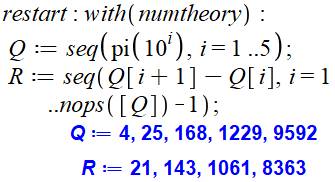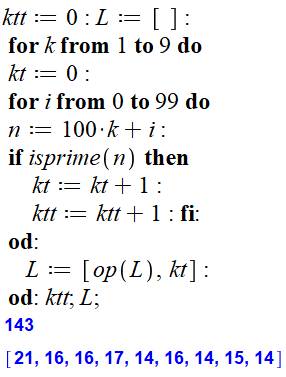|
Édition du: 30/01/2023 |
|
INDEX |
Nombres Premiers – Quantité |
||
NP: Nombres premiers
![]()
|
Quantité de NOMBRES PREMIERS Il y plus de 2 000 ans, Euclide prouva qu'il y a une
infinité de nombres premiers. Alors, deux types de
questions viennent à l'esprit : 1. Combien y a-t-il de premiers inférieurs à un nombre
donné x ? 2. Une infinité de premiers, mais quelle sorte
d'infinité ? >>> Explorons la
première question. |
||
|
|
Sommaire de cette page >>>
Les nombres premiers jusqu'à 100 >>>
Les
nombres premiers à trois chiffres >>>
Quelques propriétés >>> Ce
que nous allons développer >>>
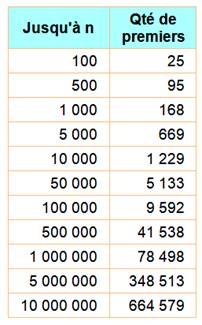
Exemple de quantités de nombres premiers >>>
Programmation >>>
English corner |
Débutants Glossaire |
|
Observations sur les
unités Le
nombre 2 est le seul premier pair:
Le
nombre 5 est le seul à être divisible par 5.
Le
nombre 3 est le seul à être divisible par 3.
On
rappelle que 1 est un nombre à part.
Bilan sur les unités Les
nombres premiers sont tous terminés par 1, 3, 7 ou
9 à
l'exception des nombres 2 et 5. Voir Crible d Ératosthène |
En jaune, les
nombres premiers jumeaux Voir Barre magique des premiers |
||||||||||||||||||||||||||||||||||||||||||
|
Quantité de nombres premiers par centaines
|
Les 143 nombres premiers à trois chiffres 101,
103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179,
181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263,
269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353,
359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443,
449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547,
557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641,
643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739,
743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839,
853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947,
953, 967, 971, 977, 983, 991, 997. |
|||||||||||||||||||||||||||||||||||||||||
|
Centaines ayant de moins en moins de nombres premiers [numéro,
quantité de premiers] [0,
25], [1, 21], [2, 16], [5, 14], [11, 12], [13, 11], [21, 10], [41, 9], [48,
8], [59, 7], [186, 6], [188, 5], [314, 4], [588, 3], [1559, 1], [16718, 0] |
Centaines comportant plus de 15 nombres premiers: [numéro, quantité de premiers] [1,
21], [2, 16], [3, 16], [4, 17], [6, 16], [10, 16], [14, 17], [42, 16], [58,
16], [194, 16], [230, 16], [7837, 17] |
|||||||||||||||||||||||||||||||||||||||||
Voir Nombre 143
Cette
propriété semble d'autant plus vraie que l'on a trouvé des premiers jumeaux
titanesques (102 259), débusqués par les supercalculateurs. |
Exemples de nombres premiers jumeaux 3 – 5 5 – 7 11 – 13 107 – 109 37 811 – 37 813 99 131 – 99 133 99 137 – 99 139. Suite en
Jumeaux |
|||
|
Comment caractériser la quantité de nombres premiers? |
Fonction Pi de n: |
|
|
Quelles sont les propriétés de cette fonction:
répartition des nombres premiers, comportement à l'infini? |
Théorème des nombres premiers >>> |
|
|
Comment approcher la démonstration concernant
l'infinité de nombres premiers jumeaux? |
Étude de l'intervalle minimum entre
premiers >>> |
|
|
Quantité (Q) jusqu'à 10n
pour n de 1 à 10 4, 25, 168, 1229, 9592, 78498, 664579, 5761455,
50847534, 455052511, Quantité (R) de 10n
jusqu'à 10n+1 21, 143, 1061, 8363, 68906, 586081, 5096876,
45086079, 404204977 Exemples: il y a 25 nombres premiers jusqu' à 100 et 21
de 10 à 100; autrement-dit: 21 premiers à deux chiffres. |
|
||
|
Quantité Q de nombre premiers jusqu'à N, avec N divisible par N. Exemple: [100, 25, 4]: il y a 25 nombres premiers
jusqu'à 100, soit un nombre sur 4. |
[2, 1, 2], [4, 2, 2], [6, 3, 2], [8, 4, 2], [27, 9, 3],
[30, 10, 3], [33, 11, 3], [96, 24, 4], [100, 25, 4], [120, 30, 4], [330, 66,
5], [335, 67, 5], [340, 68, 5], [350, 70, 5], [355, 71, 5], [360, 72, 5],
[1008, 168, 6], [1080, 180, 6], [1092, 182, 6], [1116, 186, 6], [1122, 187,
6], [1128, 188, 6], [1134, 189, 6], [3059, 437, 7], [3066, 438, 7], [3073,
439, 7], [3080, 440, 7], [3087, 441, 7], [3094, 442, 7], … |
||
Selon les
centaines
|
Quantité de premiers par centaines de rang
0 à 100 |
25, 21, 16, 16, 17, 14, 16, 14,
15, 14, 1610, 12, 15, 11, 17, 12,
15, 12, 12, 13, 1420, 10, 15, 15, 10, 11, 15, 14, 12, 11, 12, 10,
11, 15, 11, 14, 13, 12, 11, 11, 15, 9, 16, 9, 11, 12, 12, 12, 8, 15, 12, 11,
10, 10, 13, 13, 12, 10, 16, 7, 12, 11, 13, 15, 8, 11, 10, 12, 12, 13, 9, 10,
11, 9, 11, 15, 12, 10, 10, 10, 11, 10, 14, 9, 8, 12, 13, 11, 13, 9, 11, 12,
11, 11, 15, 7, 13, 11, 12, 9, 11. Ex: il y a 16 nombres premiers dans la centaine de rang 10,
soit 1000 et 1099. Ce sont: 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049,
1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097. |
|
Quantité possibles pour les centaines jusqu'à un
million |
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 21, 25 |
|
Centaines pour Q = 17 |
400, 1400, 783700, 1 023 587 Ex: Il y a 17 nombres
premiers entre 400 et 499. |
|
Centaines pour Q décroissant |
[100, 21], [200, 16], [500, 14], [1100, 12], [1300, 11],
[2100, 10], [4100, 9], [4800, 8], [5900, 7], [18600, 6], [18800, 5], [31400,
4], [58800, 3], [155900, 1], [1671800, 0] La centaine commençant par 1 671 800 est la plus petite ne contenant aucun nombre premier. Pour info, les deux premiers encadrant cette centaine sont: 1 671 781 (-11) et 1 671 907 (+7). Pas loin ! Mais dans la centaine. |
Voir Table plus
complète / Théorème
de Tchebychev (ex postulat de Bertrand)
|
Avec la fonction Pi(n)
|
But Trouver la quantité de nombres premiers à k
chiffres pour k de 1 à 5. Commentaires Réinitialisation et appel du logiciel de théorie
des nombres. Établissement s'une suite de nombres (seq) donnant la valeur de pi(n) pour les
puissances de 10 successives. La seconde séquence comptabilise la quantité de
nombres premiers ayant k chiffres. |
|
|
Sans la fonction Pi(n)
|
But Trouver la quantité de nombres premiers pour les
centaines de 1 à 9 (de 100 à 999) Commentaires Déclaration d'un compteur-totalisateur ktt. La
liste L contiendra la quantité cherchée. Une boucle pour les centaines avec un compteur
par centaines remis à 0. Une boucle pour les nombres dans la centaine. Pour chaque nombre n, on incrément les compteurs
s'il est premier (isprime). En fin de centaine, ajout de la quantité de
premiers dans la liste L. Impression de kkt,
le total et de L la liste des quantités
par centaines. |
|
Voir Programmation – Index
|
Prime counting
function: if x is a positive number, then the prime counting function,
denoted For example, since the primes up
to 10 are 2, 3, 5, 7, we have |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Table |
|
|
|
|
|
Cette page |
Renvois de liens suite à la refonte de ces
pages
|
Sur pages suivantes >>>
Fonction pi (n) >>>
Le théorème des nombres premiers >>>
Dénombrement: table des valeurs de pi (n) >>>
Méthode de recherche >>>
Historique >>>
Analyse des unités et dizaines |