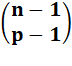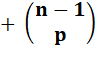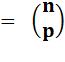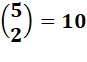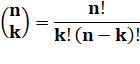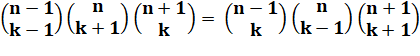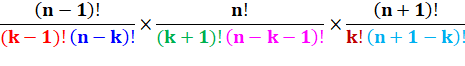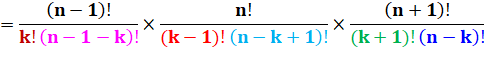NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 03/03/2021

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

             

ITÉRATIONS

 

Débutants

Général

TRIANGLE de PASCAL

 

Glossaire

Général

 

 

INDEX

Itérations

 

Approche

Formules

Propriétés

Historique

Triangle

Valeurs

Fractal

Puissance 11

Angle en Pi / n

Binôme

Divisibilité

 

Sommaire de cette page

>>> Formation du triangle

>>> Somme des entiers

>>> Somme des lignes

>>> Combinaisons

>>> Nombres de Catalan

 

>>> Nombres triangles

>>> Divisibilité

>>> Nombres de Fibonacci

>>> Progressions

>>> Triangle de Leibniz

>>> Fréquence

 

 

 

 

 

 

TRIANGLE DE PASCAL

 

Propriétés

 

Observons les propriétés des lignes colonnes ou diagonales.

 

 

 

Formation du triangle

 

Combinaisons

Chaque entrée du triangle de Pascal donne la quantité de combinaisons de p parmi n. C'est aussi la somme du nombre situé au-dessus à gauche et de celui situé au-dessus dans la même colonne, ce qui se traduit par la formule:

 

 

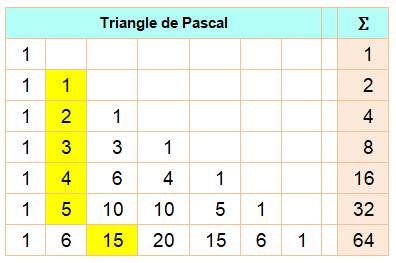
Conséquence

Avec cette disposition, chaque nombre est la somme de tous les nombres de la colonne de gauche. En effet, par exemple, 15 = 5 + 10 et 10 = 4 + 6 et 6 = …

À noter, la somme des nombres sur une ligne est la puissance de 2 du nombre en deuxième colonne (numéro de la ligne).

 

 

 

Somme des entiers

 

1

1

1

1

1

1

1

1

1

1

1

2

3

4

5

6

7

8

9

 

1

3

6

10

15

21

28

36

 

 

 

*      La 2e ligne du tableau donne la somme des n entiers jusqu'au rang considéré n.

*      Ce sont les nombres triangles

 

Exemple:

Colonne n = 7

28 = 7 + 6 + 5 + 4 + 3 + 2 +  1

 

 

 

 

Somme des lignes

 

La somme des coefficients de la ligne n donne 2n.

 

n = 5

1

5

10

10

5

1

 

 

32

= 25

n = 6

1

6

15

20

15

6

1

 

64

= 26

n = 7

1

7

21

35

35

21

7

1

128

= 27

 

 

La somme de un sur deux des coefficients de la ligne n donne 2n - 1.

 

n = 5

1

10

5

 

 

16

= 24

n = 6

1

15

15

1

 

32

= 25

n = 7

1

21

35

7

64

= 26

n = 5

5

10

1

 

16

= 24

n = 6

 

6

 

20

 

6

 

 

32

= 25

n = 7

 

7

 

35

 

21

 

1

64

= 26

 

 

Voir  Démonstration / Puissance de 2 / Pascal et Fibonacci / Brève 570

 

 

Combinaisons

 

*      Les nombres du triangle de Pascal représente les diverses combinaisons de p objets pris parmi un ensemble de n objets.

 

*      Une combinaison est un tirage une fois pour toute de n objets dans le désordre. Exemple typique le Loto.

 

Exemple:

 

*      Ce qui veut dire qu'il y a 10 possibilités de tirer 2 objets parmi 5.          Illustration =>

 

1      A  B       

2     A     C    

3     A        D 

4     A           E

5        B  C    

6        B     D 

7        B        E

8           C  D 

9           C     E

10              D  E

 

Voir Combinaisons / Factorielle

 

 

Nombres de Catalan

 

*      Les éléments centraux (en gras dans le tableau) donnent le nombre de combinaisons de n éléments parmi 2n:

 

*      Divisé par n+1, ces nombres sont appelés nombres de Catalan et, ils donnent le nombre de manières d'arranger des parenthèses, des exposants de puissance, des triangles dans un polygone, etc.

 

 Suite en  Nombres de Catalan

   

  

Nombres triangles...

 

*      Les colonnes (version triangle rectangle) ou les diagonales (version triangle isocèle) donnent successivement les nombres

*           unité,

*           naturels,

*           triangle,

*           tétraédraux,

*           etc.

*      Ce sont tous les nombres géométriques

 

 

0

1

2

3

4

1

 

 

 

 

1

1

 

 

 

1

2

1

 

 

1

3

3

1

 

1

4

6

4

1

1

5

10

10

5

1

6

15

20

15

1

7

21

35

35

1

8

28

56

70

1

9

36

84

126

1

10

45

120

210

Unité

Naturel

Triangle

Hexagonal

Tétraédriques

Pentatope

 

 

*      Un nombre est la somme de tous ceux qui sont au-dessus, sur la colonne précédente (à gauche).
Exemple: 6 (colonne 2) = 3 + 2 + 1 (colonne 1)

 

*      Triangle: empilement de pions dans un triangle (en deux dimensions).

 

*      Tétraédriques: empilement des boulets de canons sur une pyramide à base triangulaire (en trois dimensions)..

 

*      Pentatope: équivalent aux tétraédriques, mais en dimension quatre.

 

 

 

 

 

Divisibilité

 

Théorème remarquable

 

Cette propriété est à la base du Petit théorème de Fermat 

 

Les nombres des lignes où n est premier, sont divisibles par n, sauf les extrémités.

 

 

n = 3

1

3

3

1

 

 

 

 

n= 3, premier

coefficients divisibles

n = 4

1

4

6

4

1

 

 

 

 

n = 5

1

5

10

10

5

1

 

 

n= 5, premier

coefficients divisibles

n = 6

1

6

15

20

15

6

1

 

 

n = 7

1

7

21

35

35

21

7

1

n= 7, premier

coefficients divisibles

 

Voir Suite et démonstration

 

 

 

Nombres de Fibonacci:

 

Les diagonales sous-jacentes ont pour somme la suite de Fibonacci.

 

 

 

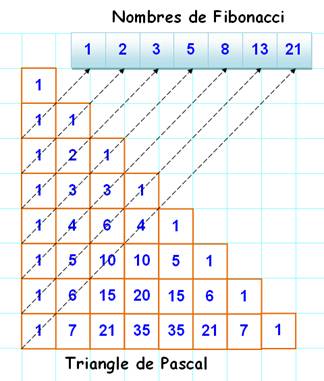
Voir Triangle de Pascal et nombres de Fibonacci / Brève 570

 

 

Progressions

 

*      Il existe une infinité de triplets en progression arithmétique:

 

           7                   21                     35

     1001               2002                  3003

490314           817190           1144066

 

*      Il n'y a pas de triplets en progression géométrique ou harmonique.

 

 

 

Fractions égyptiennes

 

*      On peut former les fractions égyptiennes (1/n)
avec les coefficients (en gras) du triangle de Pascal:

 

 

1/2

1/3

1/4

1/5

1

= 1/1

1

- 1

x 1/2

= 1/2

1

- 2

x 1/2

+ 1

x 1/3

= 1/3

1

- 3

x 1/2

+ 3

x 1/3

- 1

x 1/4

= 1/4

1

- 4

x 1/2

+ 6

x 1/3

- 4

x 1/4

+1

x 1/5

= 1/5

 

 

 

  

Triangle de Leibniz

 

*      Il existe une relation entre le triangle de Pascal et celui de Leibniz (triangle harmonique).

 

 

 

 

 

 

1/1

 

 

 

 

 

 

 

 

 

1/2

 

1/2

 

 

 

 

 

 

 

1/3

 

1/6

 

1/3

 

 

 

 

 

1/4

 

1/12

 

1/12

 

1/4

 

 

 

1/5

 

1/20

 

1/30

 

1/20

 

1/5

 

1/6

 

1/30

 

1/60

 

1/60

 

1/30

 

1/6

 

*      Chaque terme est la somme des deux du dessous
Chaque terme est égal à la fraction initiale à gauche, divisée par les coefficients du triangle de Pascal.

 

 

Exemple pour 1/4

 

Pascal

1

3

3

1

1/4 de Pascal

1/(4x1)

1/(4x3)

1/(4x3)

1/(4x1)

= Leibniz

= 1/4

= 1/12

= 1/12

= 1/4

 

 

 

 

Fréquence

 

*      Le nombre 120 est le plus petit nombre apparaissant 6 fois dans le triangle de Pascal.

 

*      Le nombre 3003 est le plus petit nombre apparaissant 8 fois dans le triangle de Pascal.
Position du 8 dans le triangle:

14 - 6

14 - 8

15 - 5

15 - 10

78 - 2

78 - 76

3 003 - 1

3 003 - 3 002

 

*      Aucun autre nombre inférieur à 223 n'apparaît aussi souvent.

David W. Wilson

 

 

 

 

 

Suite

*    Triangle de Pascal – Historique

*    Combinaisons – Toutes les formules

*    Les nombres de Pascal concaténés

*    Triangle de Pascal et relation de Fermat

*    Pascal – Biographie

Voir

*    Combinaisons

*    Formule du binôme

*    Petit théorème de Fermat

Aussi

*    Géométrie – Index

*    Récurrence

*    Théorie des nombres

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Iteration/TrgPasc3.htm