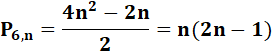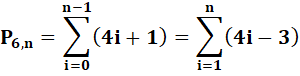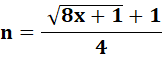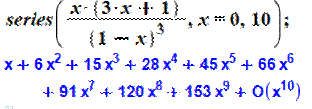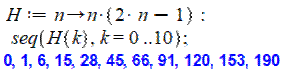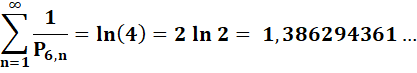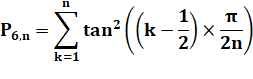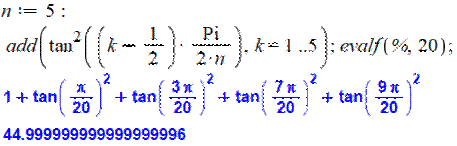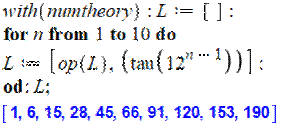Nombres hexagonaux

Édition du: 04/12/2022

INDEX Types de nombres figurés: liste et liens Nombres	Nombres Polygonaux
	Pentagonaux	Hexagonaux	Heptagonaux	Autres
	Hexagonaux de 2^e ordre et généralisés		Hexagonaux centrés
			Hexagonaux concentriques

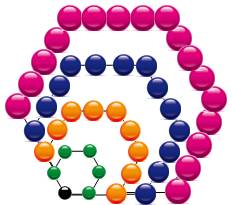
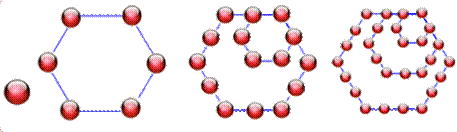
NOMBRES HEXAGONAUX

Nombres construits en déposant points sur des hexagones gigognes. L'un dans l'autre, mais avec deux côtés communs.

Sommaire de cette page

>>> Approche

>>> Propriétés avec les nombres entiers

>>> Propriétés avec le triangle de Pascal

>>> Propriétés avec les nombres triangulaires

>>> Propriétés avec les carrés

>>> Propriétés avec les nombres parfaits

>>> Propriétés avec la trigonométrie

>>> Propriétés avec les puissances de 12

>>> Langues

Débutants

Nombres figurés ou géométriques

Glossaire

Nombres géométriques

Approche		haut
Illustration Forme hexagonale	Observez que les nombres ajoutés à chaque fois sont en 4k + 1.
Notation et formules La formule en somme résulte de l'observation vue ci-dessus
Caractérisation Sorte de racine hexagonale	Si n est un nombre entier alors x est le énième nombre hexagonal. Sinon, il n'est pas hexagonal. N est une des racines de x = 2n² – n.
Fonction génératrice L'instruction demande le développement sur dix termes.
Programme
Somme des inverses
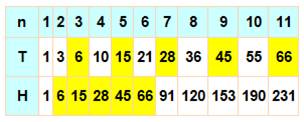
Les premiers hexagonaux	0, 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780, 861, 946, 1035, 1128, 1225, 1326, 1431, 1540, 1653, 1770, 1891, 2016, 2145, 2278, 2415, 2556, 2701, 2850, 3003, 3160, 3321, 3486, 3655, 3828, 4005, 4186, 4371, 4560, …
Les hexagonaux carrés	n, P₆, racine carrée de P₆ 25, 1225, 35 841, 1413721, 1189 28561, 1631432881, 40391 970225, 1882672131025, 1372105 32959081, 2172602007770041, 46611179 …
Les heptagonaux cubes jusqu'à n = 10⁶	n, P₆, racine cubique de P₆ 541954, 587427734278, 8375 882402, 1557265696806, 1159 …

Propriétés avec les nombres entiers

haut

Tout nombre est somme de cinq hexagonaux, sauf 11 et 26

Tout nombre plus grand que 130 est la somme de quatre hexagonaux. Le plus grand connu étant: 146 858.

Pour les nombres assez grands, trois hexagonaux suffisent.

Seules les partitions de deux nombres exigent plus de cinq nombres polygonaux:

11 = 1 + 1 + 1 + 1 + 1 + 6

26 = 1 + 1 + 6 + 6 + 6 + 6

Les vingt nombres nécessitant plus quatre hexagonaux: 5, 10, 11, 20, 25, 26, 38, 39, 54, 65, 69, 70, 78, 82, 83, 87, 93, 95, 98, 100 .

Escalier

Cette disposition en escalier produit les nombres hexagonaux (rouge) sur la dernière marche à la descente.

Chaque descente ajoute 4k + 1 marches conformément à la formule additive vue ci- dessus: 4+1 (bleu) , 8+1 (jaune) puis 12+1, etc.

Note: la diagonale 3, 10, 21, 36, 55 … donne la liste des nombres hexagonaux de deuxième ordre.

Hexagonale = Somme des (4k – 3) – Démonstration par induction

Démontrer	P_6,n = n (2n – 1)	= 1 + 5 + 9 + … + (4n – 3)
Vrai pour n = 1	P_6,1 = 1 (2 – 1)	= 1
Vrai pour n = 1 (confirmation)	P_6,2 = 2 (4 – 1)	= 1 + 5 = 6
Vrai pour n = k (hypothèse)	P_6,k = k (2k – 1)	= 1 + 5 + 9 + … + (4k – 3)
Calcul pour n = k + 1	P_6,k+1	= 1 + 5 + 9 + … + (4k – 3) + (4(k+1) – 3)
En vertu de l'hypothèse		= k(2k – 1) + (4(k+1) – 3)
		= 2k² – k + 4k + 4 – 3
		= 2k² + 3k + 1
		= (k+1) (2k + 1)
	P_6,k+1 = (k+1) (2(k+1) – 1)	= 1 + 5 + 9 + … + (4k – 3) + (4(k+1) – 3)
Conclusion	Si la propriété est vraie pour k, elle est vrai pour k+1, or elle est vrais pour 1, alors par induction, elle est vraie pour tout k.

Propriétés avec le triangle de Pascal			haut
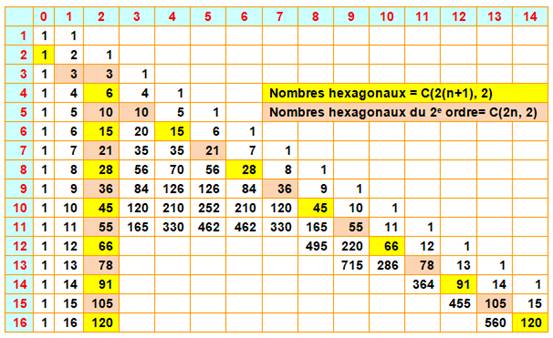
Les nombres hexagonaux sont les coefficients du binôme: combinaisons de 2 parmi 2(n + 1). Programme	Formule	Exemple
Illustration Les nombres hexagonaux généralisés représentent la 2^e colonne du triangle de Pascal: nombres hexagonaux + nombres hexagonaux du 2^e ordre

Propriétés avec les nombres triangulaires		haut
Avec les nombres triangulaires Théorème des nombres hexagonaux Un nombre hexagonal d'ordre n est égal au nombre triangulaire d'ordre 2n – 1. Soit un triangulaire sur deux (ceux de rang impair) sont aussi hexagonaux.	P_6,n = T_2n-1 = 1/2 x (2n–1) 2n = 1/2 (4n² – 2n) = 2n² – n = 4 T_n-1 + n = 4 x 1/2 x (n–1)n + n = 2n (n–1) + n = 2n² – n = 3 T_n-1 + T_n = 3/2 (n–1)n + 1/2 n(n+1) = 1/2 { 3n² – 3n + n² + n } = 2n² – n
Tout hexagonal est la somme de quatre triangulaires. Propriété générale des polygonaux, somme de triangulaires.	P_6,n = T_n + 3 T_{n – 1} = 1/2 x n(n+1)+ 3/2 n(n–1) = 1/2 (n² + n + 3n² – 3n) = 2n² – n

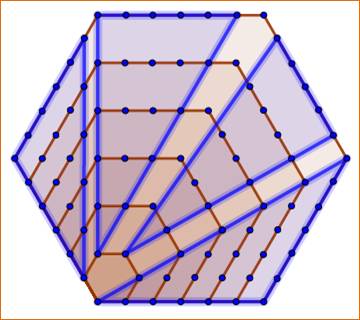
Illustration de: Hexagonal = somme de quatre triangulaires

Propriétés avec les carrés

haut

Avec les carrés de nombres successifs.

Départ avec les hexagonaux(H), puis, dans la succession des nombres, le premier du second membre est remplacé par n².

Exemple: la 20^e égalité commence par 780 et se termine par 819. La somme des carrés vaut alors: 12 466 870.

Voir Brève de maths 504

Voir Égalités semblables avec les hexagonaux due 2^e ordre

Suite: [n, premier nombre, dernier nombre, somme) ]

[2, 6, 9, 85], [3, 15, 20, 770], [4, 28, 35, 3486], [5, 45, 54, 11055], [6, 66, 77, 28171], [7, 91, 104, 61880], [8, 120, 135, 122060], [9, 153, 170, 221901], [10, 190, 209, 378385], [11, 231, 252, 612766], [12, 276, 299, 951050], [13, 325, 350, 1424475], [14, 378, 405, 2069991], [15, 435, 464, 2930740], [16, 496, 527, 4056536], [17, 561, 594, 5504345], [18, 630, 665, 7338765], [19, 703, 740, 9632506], [20, 780, 819, 12466870], …

Propriétés avec les nombres parfaits

haut

Avec les nombres parfaits

Tous les nombres parfaits sont hexagonaux.

6 = 2 (2x2 – 1)

28 = 4 (2x4 – 1)

496 = 16 (2x16 – 1)

Propriétés avec la trigonométrie

haut

Curiosité trigonométrique

Exemple avec 5

Propriétés avec les puissances de 12		haut
Curiosité avec la théorie des nombres: Un nombre hexagonal d'ordre n est la quantité de diviseurs de 12 à la puissance n – 1. Voir Nombre 12 Exemple: diviseurs de 12² = 144 => 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144 => 15 diviseurs.	Programme
Explications Nombre: 12 = 2² x 3 Puissance: (2² x 3)^n-1 = 2^2(n-1) x 3^n-1 Quantité de diviseurs: (2(n-1) + 1) n = 2n² - n	Extension Le décompte des diviseurs est valable quels que soient les nombres premiers pris à la place de 2 et 3. Le nombe 12 peut être emplacé par tout produit de deux nombres premiers dont l'un est au carré.

Langues

Anglais: A hexagonal number is a figurate number.

Allemand: Sechseckszahl oder Hexagonalzahl

Espagnol: Un número hexagonal es un numero poligonal

Italien: Un numero esagonale è un numero poligonale

Haut de page

Retour	Nombre pentagonaux
Suite	Hexagonaux de 2^e ordre Nombres hexagonaux concentriques Nombres heptagonaux
Voir	Types de nombres figurés – Index
DicoNombre	Nombre 1,386…
Sites	OEIS A000384 *- Hexagonal numbers: a(n) = n(2n-1)* OEIS A046177 - Squares which are also hexagonal numbers Hexagonal number – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/aNombre/FIGURE/Hexagone.htm