|
||||||||||||||||||||||||||||||||||||||||
![]()
|
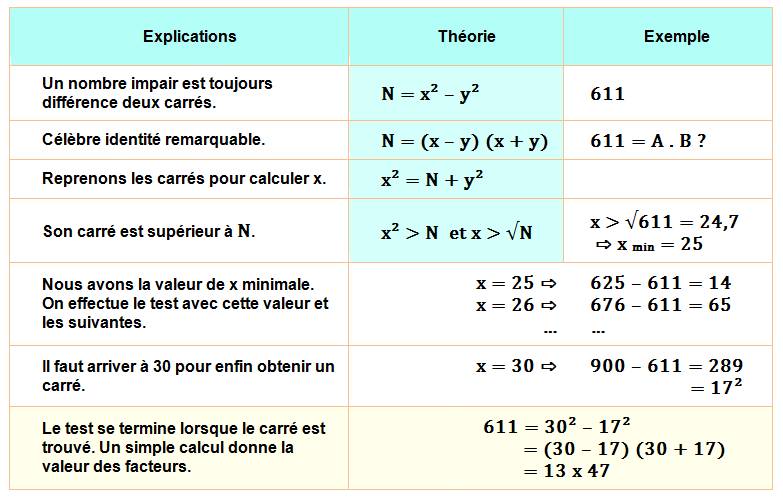
Machine à factoriser des frères Carissan Méthode du crible des résidus quadratiques Au basculement du XXe
siècle, sans l'aide des ordinateurs,
la factorisation des nombres restaient un problème
sujet à de longs calculs. Quelques
inventeurs cherchèrent à accélérer mécaniquement ces calculs. La machine des
frères Carissan et la première à avoir réalisé ce tour de force. Le calcul est basé sur la méthode de Fermat,
transformant la recherche de facteurs à celle de deux carrés. La recherche est
"écrémée" en éliminant toutes les solutions dont les restes des divisions sont incompatibles
avec ce que donne un carré. Méthode dite du crible par résidus quadratiques (reste de la
division du carré du nombre). Vous serez étonnés en lisant
cette page de constater que le principe de la machine n'est pas si compliqué
à comprendre si on connait deux choses: la division et ses restes, et une
identité remarquable très classique: x² – y²
= (x – y) (x + y). |
Anglais: Automatic sieve mechanism / Carissan
machine
|
|
|
|
Il
s'agit de la recherche des facteurs
d'un nombre N par la méthode
de Fermat. Elle consiste à
poser que le nombre (impair, car si pair il est divisible par 2) est toujours
différence de deux carrés,
donc produit de deux facteurs (Identités
remarquables).
|
|
|
|
|
|
Lorsque les facteurs sont voisins, il est possible d'utiliser des moyens
mécaniques pour effectuer le balayage des possibilités pour x (25, 26, 27 …):
c'est le cas, en particulier, de la machine des
frères Carissan, fabriquée en 1912. Le
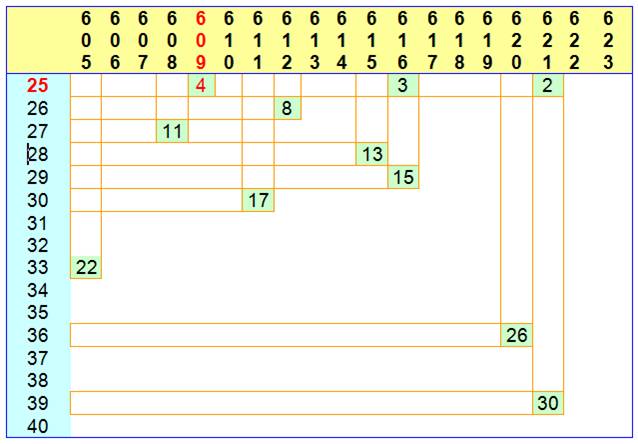
tableau montre les recherches pour 605 à 625. Par
exemple pour le nombre 609, le tableau montre une correspondance avec 25 et 4
qui conduit à la relation: 609 = 25² – 4² = (25 – 4) (25 + 4) = 21 x 29 On trouverait
aussi, non visible cette partie du tableau: 609 = 47² – 40² = 7 x 87
On
retrouve également notre exemple avec 611. On constate bien une
correspondance avec 30 et 17 qui conduit à: 611 = 30² – 17².
L'originalité
de la machine consiste à implémenter
ce genre de tableau, à mémoriser ces informations en quelque sorte. Un disque
tournant muni de picots va faire l'affaire. Mais
pas que! Un second principe est mis en œuvre pour accélérer la recherche. En
fait, une propriété qui va servir à éliminer rapidement des nombres qui de
toute façon ne sont pas des carrés. Plusieurs
disques "gigognes" tournant ensemble vont faire l'affaire. |
|
|
|
|
|
La
factorisation du nombre N procède en quatre étapes 1.
On transforme le nombre N en différence
de deux carrés x² – y² ; 2.
On identifie les nombres
possibles à travers plusieurs cribles. Cribles: on choisit plusieurs
tailles m du crible. Alors x² est divisé par m. On ne retient que les restes
possibles de cette division (résidus
quadratiques). Si seuls 0 et 3 sont possibles, on note 3.
On choisit une valeur initiale de x qui est passé aux
cribles. À défaut de répondre au critère du crible, on passe à la valeur
suivante de x. La solution est trouvée lorsque x
rempli toutes les conditions des cribles. 4.
Connaissant x, on calcule y, et finalement les deux facteurs. Illustration
Remarque
importante Les
cribles permettent d'éliminer sûrement des
valeurs pour x; mais celles qui restent dans le "tamis" ne sont que
potentiellement solutions. Plus il a de
cribles (de valeurs du modulo m) et plus la solution est cernée. De toute
façon, le calcul final des facteurs de N permet de juger de la pertinence de
la valeur trouvée. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||
|
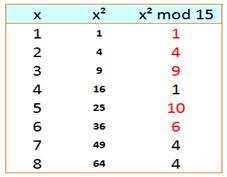
Elle
repose sur l'utilisation des résidus quadratique autrement-dit des restes de
la division des carrés par un nombre donné. |
Si x
= 10 Son carré est 100 Divisé par 7: 100 = 7 x 14 + 2 Résidu quadratique de 10 mod 7 = 2. Voir Table |
|
|
En
examinant les carrés des nombres modulo m, il se dégage des possibilités et
des exclusions. |
Avec le modulo 7, les résidus quadratiques sont
0, 1, 2, 4. |
|
|
Conséquence:
|
Un nombre n dont le résidu quadratique
modulo 7 est 3, 5 ou 6 n'est pas un carré. Dans l'autre cas, il se peut que le nombre
soit un carré. |
|
|
Balayage
sur plusieurs valeurs de m. |
Avec un examen sur diverses valeurs de m,
on élimine tous les nombres certainement non carrés. C'est le principe du
crible. |
|
|
Soit: |
N = 250 507 |
|
|
Il
faut trouver un carré avec: |
x² = 250 507 + y² |
|
|
Prenons modulo 7. |
N |
|
|
Conséquence: |
x² |
|
|
Or,
seules possibilités pour
un carré: |
x²
y²
|
|
|
Rapprochons
dans le monde du modulo. En
rouge, les deux seules valeurs compatibles. |
x² {0, 1, 2, 4} {0, 1, 2, 4} |
|
|
Donc: |
x²
|
|
|
En
revenant à x. |
x
On vérifie, par exemple, que 3x3 = 9 qui donne bien un reste de 2
lorsque divisé par 7 0, 3
et 4 sont les seules valeurs possibles. |
|
|
Prenons modulo 9 |
N |
|
|
Même
raisonnement. |
x² {0, 1, 4,
7} |
|
|
Valeurs
possibles pour x² et
pour x. |
1 1, 8 |
|
|
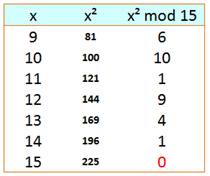
Prenons modulo 15 |
N |
|
|
Table
des restes de
la division du carré par
15. |
|
|
|
Même
raisonnement. |
x² {0, 1, 4, 6,
9, 10} |
|
|
Valeurs
possibles pour x² et
pour x. |
1 1,
4, 11, 14 |
|
|
Il
s'agit maintenant de trouver des nombres donnant ces modulos possibles
simultanément. |
Exemple: si x = 1000, alors 1000 1000 1000 Donc 100 ne passe pas le test du crible, il
est rejeté. |
|
|
Départ
de l'exploration avec racine de N car x² est supérieur à N. |
x départ = 501 |
|
|
Nous
explorons (la machine va explorer) les valeurs successives. Pour
514, 3 est bien dans la liste des possibles mod 7, comme 1 pour mod 9 et 4
dans mod15. |
501 502 503 504 … 514 |
|
|
Vérification.
Elle est nécessaire car nous n'avons utilisé que trois tests (trois modules
"m"). La
machine de Carissan en utilise 14. |
x² – 250 507 = y² y² = 514² – 250 507 = 13 689 = 117² 250 507 = (514 – 117)(514
+ 117) = 397 x 631 |
|
|
|
|
|
La machine comporte 14 disques
concentriques représentant les valeurs m des cribles pour 19, 21, 23, 26, 29,
31, 34, 37, 41, 43, 47, 53, 55, 59. Sur chacun se trouvent des picots
équidistants sur la face supérieure dont la quantité reflète les exclusions
du crible. Un engrenage dont l'axe est parallèle au
plan des disques les engrènent tous à la même vitesse. C'est en tournant la
manivelle associée que l'on fait défiler les valeurs de x. Les picots sont des solutions potentielles.
En rotation, ils passent sous une ligne d'analyse. Si une solution apparaît
du fait de l'alignement des picots sous cette ligne, un contact est établi et
un signal sonore alerte l'opérateur. La machine met, par exemple, 15 minutes
pour prouver que M31 est
premier. Une motorisation avait été envisagée pour accélérer la recherche. |
|
|
|
|
|
1876 – Lucas
écrit qu'il a inventé une machine qui serait capable de trouver les nombres
premiers qui auraient des centaines de chiffres. 1883 – Le russe I.M. Pervushin prouve que 261
– 1 est premier, contrairement à ce qu'en pensait Mersenne. P. Seelhoff le démontre
également en 1886 et idem pour J. Hudelot en 1887.
Il leur fallait plus de 50 heures pour y parvenir. 1896 – Lawrence
découvre un moyen d'automatiser la factorisation en utilisant des engrenages
et basée sur le principe d'exclusion des résidus. La machine ne fut jamais
réalisée et la description est restée incomplète. 1903 – F.N. Cole
factorise 267 – 1 et indique que cela lui a pris trois ans de
dimanches. Il en fait l'annonce à une réunion de l'American Mathematical Society en allant au tableau et en écrivant
sans commentaire: 267 – 1 = 193 707 721 x 761 838 257 287 1910 – André Gérardin publie une traduction en français des idées de
Lawrence. Ce document relance la passion pour réaliser cette fameuse machine
à factoriser. 1891 – Lucas
et H. Grenaille entreprennent la
construction de la machine ("piano arithmétique") capable de
vérifier si 2n – 1 (Nombre de Mersenne) en
quelques heures. Mais … Lucas décède sans écrit et sans la machine! 1912 – Maurice Kraitchik et A. Gérardin
imagine une telle machine. Sans qu'ils le disent cette machine ressemble de
près à celle décrite par Lawrence. 1912 – Réalisation d'un prototype de
machine à factoriser par Pierre Carissan. 1914 – T.E. Mason fait les plans d'une machine qui
appliquerait le test de primalité de Lucas aux nombres de Mersenne. 1919 – Réalisation
(un seul exemplaire) de la machine à congruences
par Eugène Carissan. C'est Eugène qui la
termine et la présente à l'exposition des machines à calculer de Paris en
1920. C'est, à preuve du contraire, la première
machine à factoriser construite et qui marche. Carissan prétend que sa
machine calcule la factorisation des nombres à dix chiffres en moins de 15
minutes. D'abord à l'observatoire de Floirac (proche de Bordeaux), elle est
aujourd'hui au musée du CNAM (Arts et Métiers) à
Paris. Les frères
Carissan: Pierre (1871-1923) et Eugène (1880-1925). 1925 – A.J.C. Cunningham et H.J. Woodall
publient des tables de factorisation des nombres de la forme Après1925 – Arrêt des recherches
intenses sur la machine à factoriser, car les calculateur de bureau sont
disponibles. On cherchera alors des méthodes qui utilisent ces machines
standards. 1932 – Lehmer propose une machine qui
calcule à raison de 5000 nombres par
seconde. |
|
![]()
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Outils/Outils/Carissan.htm |
![]()