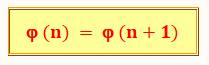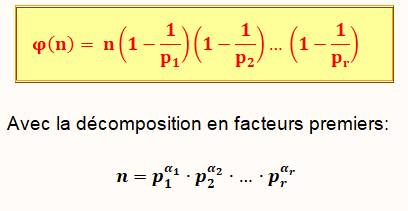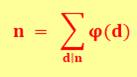|
|||||||||||||||||||||||||||||||||||||||
![]()
|
Fonction PHI d'EULER ou indicatrice d'EULER ou totient d'EULER Calculs / Opérations Phi (n) est la quantité de
nombres premiers avec n, inférieurs à n. Ses propriétés sont riches
et extraordinairement simples. |
Voir approche simple en Débutants
Rappel sur le principe du dénombrement
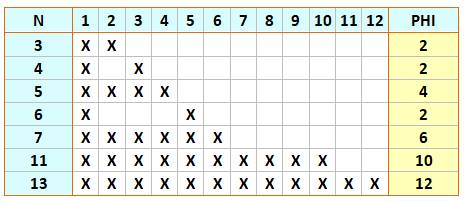
Table complète pour les nombres de 1 à 20

|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Nombre premier
C'est d'ailleurs une
condition nécessaire et suffisante pour qu'un nombre n soit premier. Nombres premiers entre eux Le totient est multiplicatif
pour des nombres premiers entre eux.
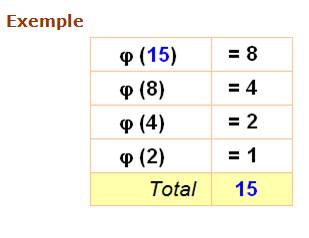
Exemple
|
Pour les nombres premiers p – phi(p) = 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
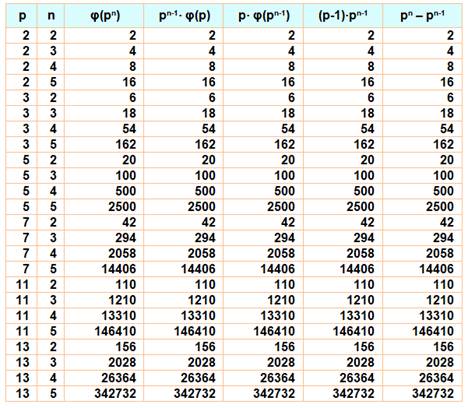
Puissance d'un nombre
premier
Exemple
|
Exemple
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
En fait,
il existe quatre formules pour la puissance de p
|
Vérification
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Nombre hautement indicateur ou totient record
|
Combien
de fois le nombre T est-il totient de n? Par
exemple: T = 72 = φ
{73, 91, 95, 111, 117, 135, 146, 148, 152, 182, 190, 216, 222, 228, 234, 252,
270}. Le nombre 72 est le totient de 17 nombres. Aucun nombre avant lui
n'atteint cette quantité. Il est Hautement-totient
ou hautement indicateur. Liste: 1,
2, 4, 8, 12, 24, 48, 72, 144, 240, 432, 480, 576, 720, 1 152, 1 440, 2 880, 4
320, 5 760, 8 640, 11 520, 17 280, 25 920, 30 240, 34 560, 40 320, 51
840, … |
Anglais: Highly totient number
Suite en Nombres hautement
indicateurs / Voir Nombres
hautement composés
|
|
||
|
|
|
|
|
Suite ci-dessous |
||
|
|
||
|
Pour tout
entier n ≥ 2, il y a au moins un autre entier différent tel que leur
totient soient identiques φ(n) = φ(m). Formulation de
Ribenboim (1996)
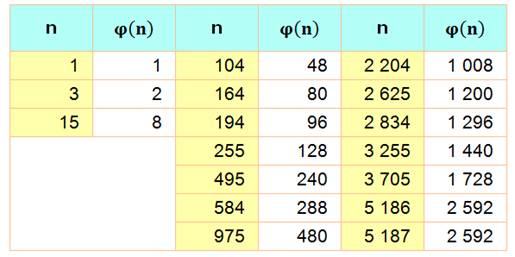
Si A(f) est la quantité d'entiers positifs n pour lesquels φ(n) =
f, alors A(f) n'est jamais égal à 1.
A(f) prend toute les valeurs possibles des entiers positifs, sauf la
valeur unité. |
Exemples
Pour chaque valeur d'un totient, il existe au moins un deuxième nombre
de même totient. Ce que l'on sait
Historique de A(f)
|
|
Voir Totient inverse / Conjectures
Référence: Carmichael's
Totient Function Conjecture
|
|
||
|
Formule
|
Exemple 10 = 2 x 5 p1 = 2 p2 = 5 φ(n) = 10 (1 – 1/2) (1 – 1/5) = 10 x 1/2 x 4/5 =
4 |
|
|
|
Calcul n = p . q φ(n) = n (1 –
1/p) (1 – 1/q) =
n (p – 1) (q – 1) /p . q =
(p – 1) (q – 1) |
|
Voir Radical d'un nombre
|
|
|||
|
Propriété
La formule se lit:
|
Exemples n = 10 d(10) = { 1, 2, 5, 10 }
φ => 1, 1, 4, 4 Somme = 1 + 1 + 4+ 4 = 10 n = 12 d(12) = { 1, 2, 3,
4, 6, 12 }
φ => 1, 1, 2, 2, 2, 4 Somme = 1 + 1 + 2+ 2 + 2 + 4 = 12 Voir Illustration |
||
|
Propriété
|
Exemple n
= 12 Premiers
avec 12 = {1, 5, 7, 11} Leur
somme s = 1 + 5 + 7 + 11 = 24 φ(12) = 4 Calcul de s s = 1/2 x 12 x 4 = 24 |
||
|
|
|||
|
Propriété
La fonction
indicatrice d'Euler est multiplicative. |
Exemples φ (10) = 4 φ (10) = φ (2) . φ (5) =
1 x 4 = 4
φ (12) = φ (3) . φ (4) =
2 x 2 = 4 Attention: Avec
des non premiers, ça ne marchent pas φ (12) = φ (2) . φ (6) =
1 x 2 ne donne pas 4. |
||
|
Propriété
|
Exemples 12
= 2 x 6 d
= PGCD(2,6) = 2 φ (12) = 2 φ (2) . φ (6) / φ (2) =
2 x 1 x 2 / 1 =
4 |
||
|
|
|||||||||||||||||||||||||||||||
|
Propriété
|
Exemples
|
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
Théorème d'Euler ou de Fermat-Euler
C'est une généralisation du petit théorème de
Fermat. Il est à la base du cryptage par le système RSA. |
Exemple m
= 5 et φ (5) = 4 a4 º 1 mod 5 pour
tout a premier avec 5
|
||||||||||||||||||||||||||||||||||
Voir Fermat / Autre généralisation d'Euler / Application: racine primitive
|
|
||
|
3, 9, 15, 27, 39, 81, 111,
183, 243, 255, 327, 363, 471, 729, 2187, 2199, 3063, 4359, 4375 …
|
|
|
Voir Nombre
parfait
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()