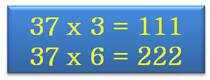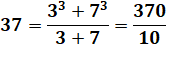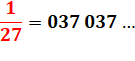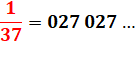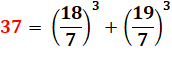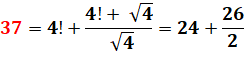nombre trente-sept en maths

Édition du: 04/05/2025

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10⁶ / 10⁹ / 10¹⁰⁰ / Infini
	-0-	10		20	30		40	50	60	70	80	90
	30	31		32	33		34	35	36	37	38	39

Nombre 37	Maths 37	Divisibilité par 37
Général 37	Répétition de motifs	Fractions curieuses
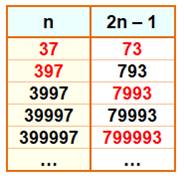
	Nombres en 371, 3711 …

Trente-sept

Thirty-seven

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	10 0101
Bases	101₆
Romain	XXX VII

Suite

Nombre réversible en lettres

Voir Strobogrammatique

Caractérisation du nombre

Binaire équilibré (autant de "0" que de "1")

Chanceux

Congruent

Coster

Cunningham

Déficient

Docile (amenable)

Emirp (37 et 73 premiers)

Fortuné

Idonéal

Impair

Lucas premier (rang)

Padovan

Palin10 (3 + 7 = 10)

Premier

Premier bon

Premier circulaire

Premier cubain

Premier cube

Premier de Chen

Premier de Pierpont 2² × 3² + 1

Premier de Pythagore

Premier fort

Premier irrégulier (n°1)

Premier résistant des deux côtés

Premier simple

Premier unique

Primeval (4^e)

Tarte ou pizza (8 coupes)

Dodécagonal centré

Hexagonal centré (4^e)

Hexagonal concentrique (5^e)

Nombre étoilé (3^e)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Propriétés MATHÉMATIQUES

Chiffres et numération

37 – 3 – 7 = 27 =3³ 37 – (3 × 7) = 16 = 2⁴ 37 × (3 × 7) = 777 37 × 73 = 2 701 = T₇₃ 73 – 37 = 36 = T₈	Opérations avec ses chiffres qui donnent: cube, bicarré, repdigit et triangulaires.
37 × 3 = 111	Devient repdigit en le multipliant par 3.
	Nombre n qui engendre son retourné avec 2n – 1. Le motif est infini en intercalant des 9. 37 et 73 est le seul couple de premiers (rouges). 14 et 41 est le seul couple avec la relation 3n – 1. 247 et 742 est les eul avec la relation 3n + 1. Aucun couple en kn ± 1 avec k > 3. Notez la somme palindromique en nombres: 37 + 73 = 0110 = 73 + 37
37₁₀ = 211₄ = 122₅ 37₁₀ = 52₇ = 25₁₆ 37₁₀ = 41₉ = 14₃₃ 37₁₀ = 31₁₂ = 13₃₄ 37₁₀ = 21₁₈ = 12₃₅	Mêmes chiffres dans deux bases différentes, Cinq fois. Plus petit cas.
37 = 12 + 25 = 2 + 5 + 30 & 12 x 25 = 2 x 5 x 30 = 300	Deux solutions pour S = 37 et P = 300. Cas rare.
37 = ( 3² + 7² ) – (3 x 7 ) = 58 – 21	Curiosités avec les chiffres de 37. Division curieuse (seule avec 48 pour deux chiffres).
37 = 4 + 9 + 24	Masse du nombre DIX.

Repdigits et 37 – Occasion de jolis motifs

Propriété: Un repdigit de trois chiffres est divisible par la somme de ses chiffres.

Voir Repdigits / Pépites / Nombre 666 (de la Bête)

Addition et soustraction

37 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 9

Partition unique avec huit chiffres différents.

Exemples de partitions en somme palindrome.

Les deux premières lignes: palindromes en nombres.

Les deux suivantes, purs palindromes en chiffres.
Il existe 297 telles sommes palindromes pour 37.

Multiplication, division, diviseurs

Cinquante multiples de 37

37, 74, 111, 148, 185, 222, 259, 296, 333, 370, 407, 444, 481, 518, 555, 592, 629, 666, 703, 740, 777, 814, 851, 888, 925, 962, 999, 1036, 1073, 1110, 1147, 1184, 1221, 1258, 1295, 1332, 1369, 1406, 1443, 1480, 1517, 1554, 1591, 1628, 1665, 1702, 1739, 1776, 1813, 1850.

37-Harshad = [111, 222, 333, 370, 407, 444, 481, 518, 555, 592, 629, 666, 777, 888, 999]		Ces quinze nombres sont 37-Harshad. Quotient 37 lorsque divisés par la somme de leurs chiffres. Rare et sans doute la plus grande quantité.
37 et 73 sont premiers		Premiers circulaires ou permutable ou EMIRP.
3, 7, 37, 73 sont premiers		Nombre multi-premier. Toutes les combinaisons des chiffres de 37 sont des nombres premiers. Le suivant: 113 Voir Brève 760
37 > (31 + 41) / 2		Premier fort.
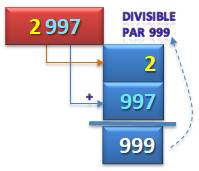
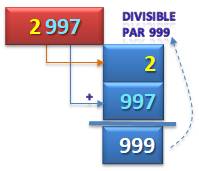
37 premier 39 = 3 x 13 semi premier		37 est le 12^e premier, alors que son retourné 73 est le 21^e, le rang retourné. Seul cas jusqu'à, au moins, le millionième premier. Nombre premier de Chen. Le plus grand idonéal premier. Aussi premier irrégulier.
		Clé de divisibilité par 37. Constituer des blocs de 3 chiffres et les additionner. Le résultat doit être divisible par 37. Avec cet exemple: 2 997 est divisible par 999 et par tous ses diviseurs: 1, 3, 9, 27, 37, 111, 333, 999 dont 37.
		Les restes de la division par 37 des puissances de 10 forment un cycle {1, 10, 26} que l'on peut aussi écrire {1, 10, -11} avec 26 – 37 = –11 Propriété exploitée pour tester si un nombre est divisible par 37.
		Curiosité due au fait que 27 × 37 = 999. Propriété que l'on retrouve pour les nombres en 10ⁿ – 1.
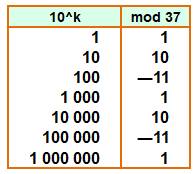
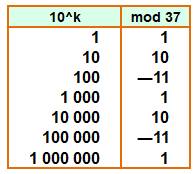
37 = 111 / 3 = 222 / 6 = 111 111 / 3 003 = 222 222 / 6 006 = 111 111 111 / 300 300 3 = 222 222 222 / 600 600 6 = …		Repunits divisibles par 37 et, par conséquent les repdigits correspondants. Voir Divisibilité par 37
37 = aaa / 3a		aaa = nombre à 3 chiffres identiques (repdigit). Un nombre *aaa* , formé de trois chiffres identiques est divisible par 3, 37 et par 111.
37, 371, 3711, 37111, …		Tous ces nombres après 37 sont composés, et 37 est le plus petit nombre produisant cette propriété.
37 x 5 = 185 et 851 = 37 x 23 et 518 = 37 x 14		Pour tous ses multiples à 3 chiffres, la permutation circulaire des chiffres est divisible par 37.
37 = 223 092 907 – 223 092 870		Nombre fortuné: différence entre primorielle et le premier juste plus grand (d'au moins 2).
	Le nombre de classe de ce corps quadratique est 2. Ce corps contient tous les nombres de la forme a + ib avec a et b rationnels. Il existe 18 tels corps avec k = 5, 6, 10, 13, 15, 22, 35, 37, 51, 58, 91, 115, 123, 187, 235, 267, 403, 427. OEIS A005847 / Table

Avec les puissances

37 = 2² + 2² + 2² + 5²	Somme des carrés de quatre nombres premiers.
37 = 1² + 6² = 1² + 2² + 4² + 4² = 2² + 2² + 2² + 5² = 1² + 1² + 1² + 3² + 5² = 1² + 3² + 3² + 3² + 3² = 1² + 1² + 1² + 3² + 3² + 4²	Les autres sommes de carrés jusqu'à six termes.
37 = 1³ + 1³ + 2³ + 3³	Somme de cubes. Unique jusqu'à quatre termes
37 = 4 + 8 + 9 + 16	Somme de quatre puissances consécutives.
37 = 19² – 18² = 19 + 18	Motif général pour tout nombre impair.
	Somme de deux cubes rationnels.
37 = 4³ – 3³ = 64 – 27	Nombre binomial. Premier, différence de deux cubes successifs; tous de la forme 6k+1. Voir Type de premiers
37 => x⁵ + … + z⁵	Tout nombre est la somme de, au plus, 37 nombres à la puissance 5. Voir Théorème de Waring

En puissance

37² + 3 = 2² x 7³ = 1 372	Nombre tel que n² + 3 est un nombre avec facteur carré. Le plus petit. Suivants: 79 196, 177 833 … Liste infinie (Florian Luca).
37² = 12² + 35² = 144 + 1225 = 1369	6^e triplet de Pythagore primitif.
	Carré concaténation de trois carrés.
37³ = 107² + 198² = 37² + 222²	Cube somme de deux carrés.

Dénombrement, jeux et curiosités

37 = ½ (8 x 9) + 1	Nombre tarte: quantité maximale de parts de tarte obtenue en la coupant avec 8 coups de couteau.
37 Quantité de régions dans un carré partagé. Les côtés sont partagés en 3 segments. Chaque point est relié au point situé 4 pas plus loin à la façon d'un dessin de fils tendus. Tous ces segments partagent le carré en 37 régions.
		Jeu du quatre 4.

Autour du nombre

1, 7, 19, 37 … 37 = 1 + 6 + 12 + 18	Nombre hexagonal centré (4^è).
37 = 7 x 7 – 3 x 4 = 7² – 3x2² = 5² + 3x2²	Nombre du solitaire octogonal.
37	Nombre chanceux d'Ulam.
37 x 36 / 2 = 666	Nombre de la Bête.
a⁵ + b⁵ + … + n⁵	Tout nombre est la somme d'au plus 37 puissances cinquièmes.
2^a – 3^b	Il existe 37 nombre inférieurs à 100 atteints par cette formule.
		Les multiples de 3 multipliés par 37 produisent les repdigits dont la somme des chiffres est le multiple de3.

37! = 1,376375309... 10⁴³	Factorielle 37 compte 44 chiffres et parmi eux on trouve deux fois le nombre 37.
37! + 1	Générateur de nombre premier factoriel. Factorielle plus 1 donne un nombre premier.
1 / 37 = 0,027 027 027 … 1 / 27 = 0,037 037 037 … Explication 37 × 27 = 999	Nombre périodique. Le seul de longueur 3. 37 est un nombre premier unique.
		Toutes les fractions avec 37 au dénominateur possèdent trois décimales répétitives en douze suites permutées. Le plus petit nombre avec douze suites.