NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/01/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	GRANDS ESPRITS Savant
Débutants Général	PYTHAGORE		Glossaire Général
Sommaire de cette page >>> Pythagore >>> Philosophie & arts >>> Maths >>> Sciences & musique >>> réalités ou légendes

Humour

Voir Pensées et Humour / Einstein

Mysticisme des nombres

« Tout est nombre »

Les nombres sont le principe des choses, de l’harmonie universelle.

Tout un édifice …	Avec des imperfections!
10 = 1+2+3+4 est sacré fractions (commensurabilité) nombre d'or dans l'étoile à 5 branches gamme musicale sphères célestes	0 est à rejeter 2 ne doit pas être dévoilé

Voir Everything is number – Citations

PYTHAGORE

vers 570 / 495 av. J.-C. - 85 ans

Selon le Larousse (il existe de nombreuses autres dates)

Mémorisons – 500

Philosophe et mathématicien grec

responsable d'importants développements en

mathématiques, astronomie et musique

Vie peu connue: figure mythique.

Œuvres connues que de façon indirecte.

Parmi ce qu'il a fait:

Affirme que la Terre et une sphère;

La pensée nait dans le cerveau et non dans le cœur;

Invente les mots "philosophie" et "mathématiques";

Démontre le théorème qui portera son nom: a² + b² = c². C'est certainement la première démonstration de l'histoire;

Défend la beauté tout autant que la logique des nombres;

Croyance mystique accordée aux nombres: musique, nature, cosmos …

Biographie

Né sur l'île de Samos comme Archimède (deux siècles plus tard).

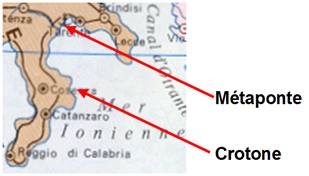
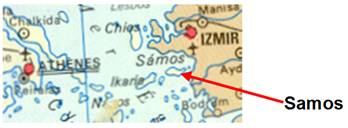
Proche de côtes turques en face de la Grèce.

À 18 ans participe aux Jeux Olympiques.

En secret, il quitte Samos et son tyran Polycrate pour se réfugier chez son oncle sur l'île de Lesbos. Il est instruit par le philosophe Ferekid, alors aussi réputé que Thales.

Il rencontrera Thalès alors âgé de 90 ans.

Il va étudier la cosmographie, la physique et les mathématiques.

Voyage en Syrie, Égypte (20 ans), Babylone (12 ans), et Inde (sans doute).

En Égypte il apprend et se fait apprécier des prêtes.

À 40 ans (environ), il retourne à Samos où règne le tyran Polycrate; il s'exile dans une caverne.

Il part ensuite pour Crotone dans le sud de l'actuelle Italie (Calabre).

Sous la protection de Milon, un richissime habitant, il fonde une Fraternité proche d'une secte.

Il se marie avec Théano, une de ses élèves, la fille de son protecteur.

Un candidat recalé Cylon, pour se venger, attisa la population de Crotone pour détruire la Fraternité. Pythagore et plusieurs de ses disciples y périrent.

Mort à Métaponte.

Ville alliée de Crotone, proche de Tarente.

Lieux

Voir Carte complète

Contemporains de Pythagore

Zarathoustra Zoroastre	En Perse (Iran) => Les Parsis en Inde	628-551 av. J.-C.
Lao-Tseu Laozi	Philosophe taoïste chinois	Un peu plus âgé que Confucius
Bouddha	Sage indien Parvenu à l'éveil (bodhi)	560-480 av. J.-C.
Confucius Kongzi	Sage chinois	551-479 av. J.-C.

Voir Contemporains – Chronologie

Anglais : Pythagoras, the Pythagoreans

Philosophie et Art

Philosophe: celui qui cherche à découvrir les secrets de la nature de façon désintéressée.

Pythagore invente le mot et se définit comme philosophe.

Il fonde une confrérie basée sur les mathématiques:

appelée: École de Pythagore ou Fraternité pythagoricienne

association scientifique, philosophique, politique et religieuse avec règles de vie et d'éthique.

Philosophes qui veulent expliquer le monde par les mathématiques et le nombre.

Ses disciples s'appelaient les mathématiciens.

Mathématique signifiant en grec ancien, la science, ce qu'on enseigne ou qu'on apprend.

Les textes sont secrets, accessibles que par les initiés.

Et tout en oral: il fallait une bonne mémoire.

Deux catégories de disciples:

Acousmaticiens (auditeurs) qui n'avaient que les résultats,

Mathématiciens: résultats et démonstrations.

Il donne une interprétation mystique aux nombres attribuant

un nombre à chaque chose,

une correspondance entre les nombres et les mécanismes de la nature.

Mysticisme des nombres: « Tout est nombre ». Les nombres sont le principe des choses, de l’harmonie universelle

Adepte de la métempsycose:

Renaissance, réincarnation et plusieurs vies;

Transmigration des âmes, doctrine d'origine indienne.

Activités politiques:

Contre l'anarchie.

Pour théocratie, aristocratie, conservateurs.

Maths

Arbre de Pythagore

Fractales composées de carrés qui se divisent en deux carrés à 45°;

Arithmétique

Les Pythagoriciens développent l'arithmétique et furent, selon Aristote,

Les premiers qui firent progresser les mathématiques

Nombres

Tout est nombre: entier ou fraction

Tout dans la nature se ramène à un nombre

Pair Impair

Spéculations autant mystiques que scientifiques

Décade de Pythagore

Il donne une interprétation mystique aux nombres attribuant un nombre à chaque chose:

Zéro

Refus

du zéro qui n'avait pas de représentation géométrique

On ne peut pas dessiner un carré dont l'aire est 0

également et par conséquent, du vide

Dix

Nombre sacré:

Symbolise les pouvoirs divins

Nombre triangulaire

1 + 2 + 3 + 4 = 10

Table de Pythagore

Table de multiplication à double entrée

X	1	2	3	4	5
1	1	2	3	4	5
2	2	4	6	8	10
3	3	6	9	12	15

Voir Table en DicoMot Math / Table de Pythagore et polygones

Nombres figurés

Les nombres sont figurés par des assemblages de points: triangle, carrés, pentagone...

Irrationnel

La diagonale du carré ne contient pas un nombre entier de fois le côté

Du coup, la nature n'attribuerait pas forcément un nombre entier (ou une fraction) à toute chose!

Crise suite à cette découverte de l’incommensurabilité de la diagonale du carré (2)

Cette découverte est attribuée à Hippase de Métaponte

Il divulgue sa découverte

Et, périt dans un naufrage.

Nombres parfaits

Nombres amicaux

Somme des diviseurs redonne le nombre

Somme des diviseurs de l'un donne l'autre

Théorème de Pythagore

Triplets de Pythagore

Connu bien avant lui par les Babyloniens

Un triangle de côtés 3, 4 et 5 est rectangle (triangle isiaque)

et en général pour un triangle rectangle:

c² = a² + b²

On ne sait pas si Pythagore a démontré ce théorème qui porte son nom

On a tout de même sacrifié 100 bœufs (une hécatombe) aux dieux en hommage à cette relation

Angle du triangle

Ils démontrent que la somme est égale à 180°

Solides platoniciens

Construction des 5 seuls polyèdres réguliers

Pentacle

Figure formée du pentagone et de l'étoile à cinq branches

On peut inscrire l'un dans l'autre à l'infini

Contient le nombre d'or de multiple fois

Emblème sacré des pythagoriciens

Nombre d'or

Découverte de ce rapport idéal

L'un des 10 rapports de la table d'harmonie des pythagoriciens

Le nombre d'or forme les plus belles figures

Mais, il présente un inconvénient majeur: il est irrationnel comme 2 …

Théorie des proportions

Rapport comparé entre la taille de objets: commensurabilité: fractions

Moyenne harmonique

Inventée par Hippase de Métaponte

1/m = 1/a + 1/b

Démonstrations

Ils sont les premiers à développer les démonstrations

Basées, il est vrai, sur des dessins à la règle et au compas

Sciences et musique

Théorie des intervalles musicaux et étude des astres.

Rapports entiers simples

Les Pythagoriciens extrapolent en pensant que le monde est le reflet des mathématiques.

Quand Pythagore vérifie qu’une corde entière de lyre donne un do, que trois quarts de la corde donnent un fa et deux tiers donnent un sol, il consolide son intuition que la nature est mathématique, il renforce sa conviction que tout est nombre.

Musique

Les vibrations des cordes produisent des sons harmonieux

quand les rapports des longueurs des cordes sont des entiers

et cela est transposable à tous les instruments

Utilisation du monocorde pour développer leur philosophie

Monocorde: (sorte de tympanon) boîte de résonance avec une seule corde tendue et un chevalet mobile (sorte de capodastre)

Selon le rapport des distances, on obtient deux notes: une grave et une aiguë

Cas du milieu: les deux notes sont identiques à l'octave du son produit par la corde complète (le fondamental). L'octave correspond au rapport 1/2

Avec le rapport 1/3, l'autre côté étant 2/3, on obtient deux sons à l'octave l'un de l'autre puisque l'un des deux côtés est deux fois plus long que l'autre

Avec ce rapport, le côté 2/3, le plus long, "sonne bien" avec le son fondamental donné par la corde entière. L'intervalle obtenu entre les deux sons constitue la quinte, un accord très harmonieux

Pourquoi ne pas continuer pour obtenir d'autres sons harmonieux en recoupant chaque partie en 2/3

On obtient en effet deux nouvelles quinte à 4/9 et 8/9

Les rapports sont de la forme générale 2ⁿ / 3^m

En pratique, on divise autant de fois que nécessaire jusqu'à ce que le rapport soit proche de 1 (il n'est malheureusement jamais égal à 1).

Voici quelques valeurs retenues dans l'histoire:

n	m	2^n / 3^m	Nom & correspondance
8	5	1,053497942	Pentatonique => 5 touches noires du piano
11	7	0,936442615	Heptatonique => 7 touches blanches du piano
19	12	0,986540369	Chromatique => 12 toutes les touches du piano
84	53	0,997914046	53 notes de la gamme des solfèges
1054	665	0,999956346

Sciences

Premier à classer les astres connus de l'époque:

Soleil, Lune, Mercure, Vénus, Mars, Jupiter et Saturne

Selon leurs distances supposées à la Terre

Tentent d'accorder distances et périodes de révolutions,

Avec les intervalles musicaux,

Concept des sphères célestes et de leur mélodie.

Sa cosmologie est basée sur les nombres comme l'harmonie de la musique.

La Terre est une sphère

et non pas un disque flottant dans l'air,

comme dans le modèle d'Anaximandre.

Soleil, Lune et planètes

tournent autour de la Terre,

se déplacent sur des orbites harmoniques

en cercles concentriques attachés chacun à une sphère;

une sphère ultime supporte les étoiles fixes;

ces sphères émettent une mélodie de plus en plus aiguë pour les plus lointaines;

l'ensemble produit l'harmonie des sphères célestes.

Le premier à penser que les astres obéissent à des lois qui se concrétisent en nombres.

Pythagore invente le mot "cosmos" qui veut dire "ordre".

Le premier à reconnaître la même Vénus dans l'étoile du matin et du soir.

La lumière

est émise par des corps lumineux,

elle peut se réfléchir et

elle est vue lorsqu'elle entre dans l'œil.

Résumé

Les pythagoriciens ont généralisé des observations fortes sur l'harmonie musicale et sur l'harmonie des sphères en astronomie. Ils développent une théorie des contraires, basée sur l'opposition pair-impair (féminin-masculin, etc.). S'ils considèrent l'air, l'eau, le feu et la terre comme élémentaires, ce sont, dans leur conception des intermédiaires entre les nombres et les substances. Ils rattacheront les polyèdres à ces éléments, conception qui sera reprise par Platon.

Claude Lécaille – L'aventure de le chimie jusqu'à Lavoisier

– page 13 – Vuibert - 2004

Réalité ou légendes
Réincarnation	Pythagore se croit la réincarnation d'Euphorbe, un héros troyen.
Vie	Manger cru et végétarien. Boire de l'eau. Ne pas s'habiller de laine. Faire l'amour en hiver.
Haricot	À proscrire: donne des flatulences et ressemble aux organes génitaux. Pythagore se serait fait tuer plutôt que de traverser un champ de haricots pour s'enfuir.
Constitution	Pythagore aurait écrit la constitution en vigueur en Italie de l'époque.
Hippase	Il aurait été condamné à la noyade pour avoir révélé le secret de l'existence des nombres incommensurables.

Voir	Théorème de Pythagore – Démonstrations Triplets de Pythagore Briques de Pythagore Décade de Pythagore Escargot de Pythagore Années Pythagore Triangle isiaque
Aussi	Contemporains de Pythagore Nombres figurés - Débutants Nombre figurés - Index Nombres parfaits Nombres amiables Carrés magiques Formule de la relativité Géométrie - Index
Sites	Pythagore - complet et illustré Pythagore - Bibmath Pythagore - Encyclopédie Agora Pythagore - encyclopédie Yahoo Pythagore - l'écran des maths Pythagoras - from Eric Weisstein Monocorde
Livre	Zéro - La biographie d'une idée dangereuse Un bon tour d'horizon de l'histoire des maths à travers du concept du zéro d'hier à aujourd'hui La vie de Pythagore par Porphyre de Tyr.
Cette page	http://villemin.gerard.free.fr/Esprit/Pythagor.htm