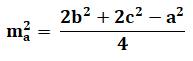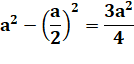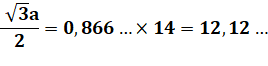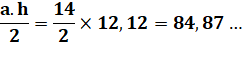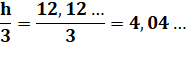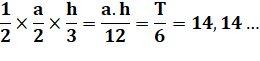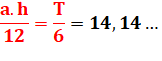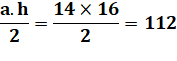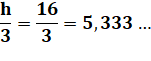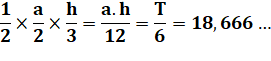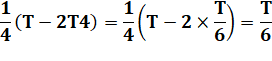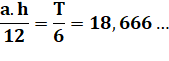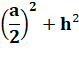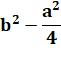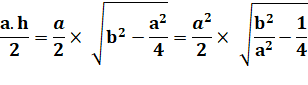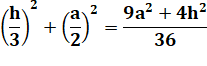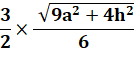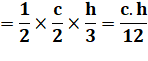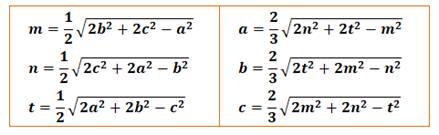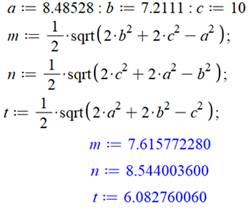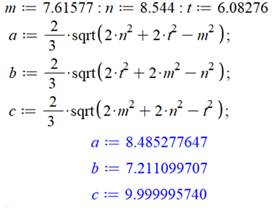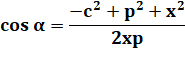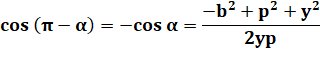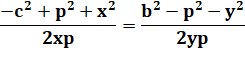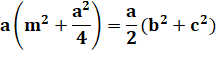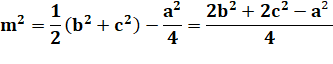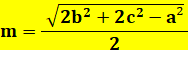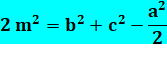triangles et médianes

Édition du: 01/09/2022

INDEX Types de triangles Triangle Géométrie	Triangle: Droites remarquables
	Droites et points	Bissectrices	Médianes – Propriétés (1)
	Point Milieu	Médiatrices	Médianes – Partage (2)
	Point et triangles	Hauteurs	Médianes – Démo (3)
	Distances	Triangle médian	Médianes – Démo vecteurs (4)
	Céviennes régulières		Médianes – Démo autres (5)

MÉDIANES du TRIANGLE (1/5)

Quelques propriétés remarquables des médianes des triangles et le centre de gravité.

On trouvera d'autres propriétés lors de l'exploration des démonstrations sur les pages suivantes.

Les trois médianes d'un triangle se rencontrent en un point unique, le centre de gravité du triangle.

Chaque médiane partage le triangle en deux triangles de même aire.

Les trois médianes partagent le triangle quelconque en six triangles de même aire.

A savoir

Dans le triangle quelconque

Sommaire de cette page

>>> Triangle équilatéral

>>> Triangle isocèle

>>> Triangle quelconque

>>> English corner

>>> Bilan

>>> Théorème des médianes

>>> Longueur des médianes et des céviennes

Débutants

Géométrie

Glossaire

Médianes

Triangle

Voir Propriétés fondamentales des triangles

Médianes du triangle équilatérals		haut
Triangle équilatéral ABC de côté a = 14 carreaux. La notation T ou Ti veut dire aire du triangle T ou Ti.
Sa hauteur mesure (Pythagore):	h² =
Valeur numérique:	h =
Aire du triangle:	T =
Longueur de GC':	GC' =
Aire de T4 ou T5:	T4 =
Le triangle étant équilatéral, les six triangles sont égaux car ils ont tous, de deux en deux, un côté en commun, un côté égal et un angle égal.	Ti =

Médianes du triangle isocèle			haut
Triangle isocèle ABC de côté a = 14 carreaux. Longueurs données (figure ci-contre): a = 14 carreaux h = 16 carreaux
Aire du triangle du triangle isocèle:	T =
Longueur de GC':	GC' =
Les triangles T4 et T5 sont égaux du fait de la symétrie. Leur aire:	T4 = T5 =
Les triangles T1 et T2 sont égaux du fait également de la symétrie du triangle isocèle.	T1 =	T2
Dans le triangle CGA, la médiane GB' partage ce triangle en deux triangles de même aire.	T1 =	T6
En rapprochant les égalités:	T1 =	T2 = T6 = T3 (en aire)
Partage du grand triangle:	T =	2T4 + 4T1
Aire de T1:	T1=
Conclusion, même dans le triangle isocèle, les six triangles ont la même aire.	Ti =

Le côté b mesure:	b² =
Soit la mesure de h en fonction de a et b.	h² =
Aire du triangle en fonction de a et b.	T =
Longueur de AG, qui vaut les 2/3 de la médiane AA':	m² =
Longueur de la médiane:	AA' =

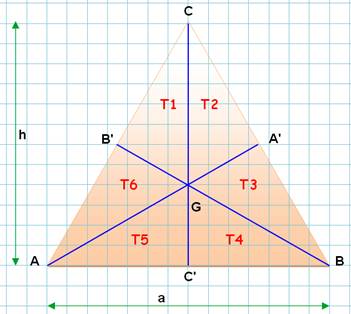
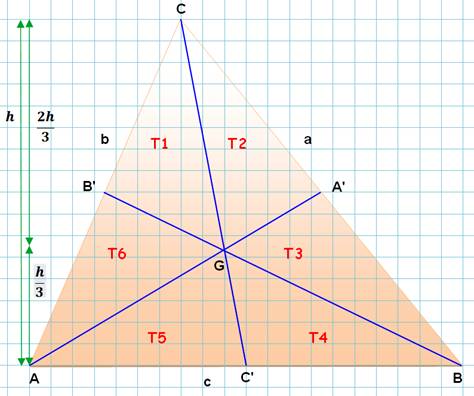
Médianes du triangle quelconque				haut
Triangle quelconque ABC de côté a = 14 carreaux. De côté a, b et c. Médianes AA', BB' et CC'. Théorème des médianes Pour tout triangle, la somme des carrés des médianes est égale aux trois quarts de la somme des carrés des côtés.	Voir Triangle médian
La médiane CC' partage les triangles ABC et AGB en deux triangles d'aires égales.		T1 + T6 + T5 T5 T1 + T6	= T2 + T3 + T4 = T4 = T3 + T4
Le point G est situé au 2/3 de CC'. *La proportion est conservée sur la hauteur (Voir* Proportion 2 : 1)**		2T5	= T1 + T6
Avec la médiane GB':		T1	= T6
En rapprochant:		2T5 T5	= 2 T1 = T1 = T6
Idem pour l'autre côté:		T1 + T2 + T3	= T4 + T5 + T6
Et pour le calcul de l'aire de chacun:		Ti

Théorème

Les trois médianes concourent en un même point G, le centre de gravité. Elles divisent le triangle en six triangles de même aire.

Theorem: The three medians of any triangle intersect in one point, G, called the centroid. Furthermore, the medians divide the triangle into six triangles of the same area.

Voir Partage du triangle / Démonstration du théorème

English corner

Triangles T5 and T4 have the same altitude since they share the same vertex and are sitting on the same base AB.

But we know that C' is the midpoint of AB (CC' is the median).

It then follows that the area of triangle T5 is equal to the area of triangle T4.

We know that in the case of two medians, the second median divided the two triangles formed by the first median in the ratio 2:1. Using that argument we know that the area of triangle T5 is 1/3 the area of triangle ACC'.

Similarly the triangles T6 and T1 are also equal in area. This means that the area of triangle T6 = area of triangle T1 =1/3 area of triangle ACC'.

We can now conclude that the triangles T1, T6 and T5 are all equal in area.

Same for right part: T2, T3 and T4 are all equal in area.

Bilan

Chaque médiane partage le triangle quelconque en deux triangles de même aire.

Les trois médianes partagent le triangle quelconque en six triangles de même aire.

Le point de concours des médianes est le centre de gravité (centroid). Ce point partage la médiane dans le ratio 2 : 1.

Le triangle tient en équilibre sur son centre de gravité ainsi que sur les lignes médianes.

Théorème des médianes		haut
Théorème des médianes Pour tout triangle, la somme des carrés des médianes est égale aux trois quarts de la somme des carrés des côtés. Démonstration m² = h² + d² h² = a² – HB² = a² – (c/2 – d)² h² = a² – c²/4 + cd – d² m² = a² – c²/4 + cd h² = b² – AH² = b² – (c/2 + d)² h² = b² – c²/4 – cd – d² m² = b² – c²/4 – cd Somme de ces deux égalités 2m² = a² + b² – c²/2 Pour les deux autres médianes n et t 2n² = c² + a² – b²/2 2t² = b² + c² – a²/2 Somme pour les trois médianes 2(m² + n² + t²) = 2(a² + b² + c²) – 1/2 (a² + b² + c²) 4(m² + n² + t²) = 3(a² + b² +c²)	3(AB² + BC² + CA²) = 4(AE² + BD² + CF²) Formules des longueurs
Exemples de calculs pour vérification	Attention: les notations sur cette figure correspondent bine aux noms calculés dans les formules

Voir SUITE généralisée ci-dessous

Voir Propriétés métriques des médianes

Merci à Arnaud Piquerez pour ses remarques

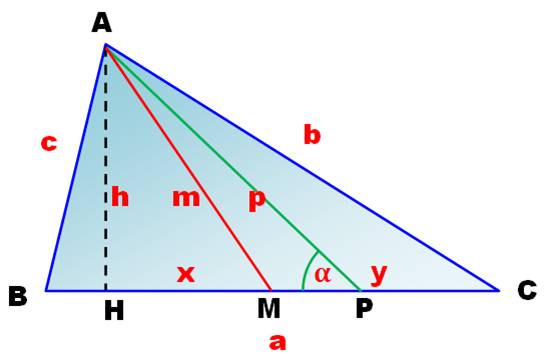
Longueur des médianes et des céviennes Théorème d'Apollonius Théorème de Stewart (1946)
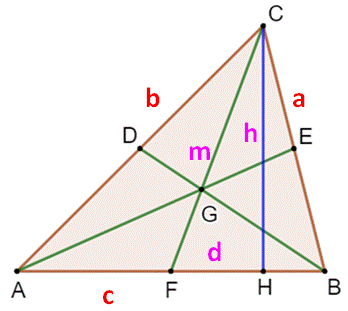
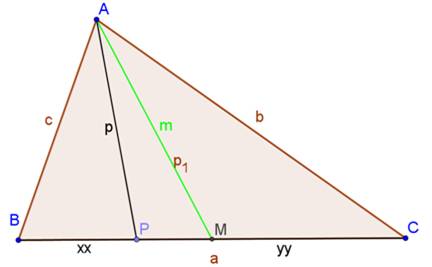
Figure AM est la médiane de longueur m. Ap est une cévienne de longueur p dont le pied est à une distance x du sommet
Relation dans les triangles APB et APC.
Égalité des cosinus. Puis, en simplifiant directement par 2p.
Théorème de Stewart donnant la longueur de la cévienne p.
Cas de la médiane avec x = y = a/2. Avec sa forme commune: Théorème d'Apollonius
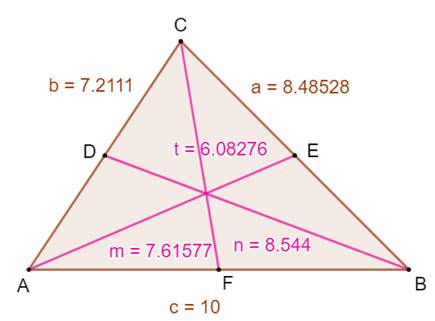
Vérification avec GeoGebra Les points bleus indiquent les cordonnées ou les mesures relevées par GeoGebra. Les lignes 1 et 2 montrent la vérification de la relation pour les céviennes. La ligne 3 montre le calcul de la longueur de la médiane et la ligne 4 donne la mesure faite par GeoGebra.

Merci à Daniel F. pour avoir rappelé ces théorèmes et signalé la page allemande en référence

SUITE: les médianes sont concourantes – Démonstrations (page 3/5) >>>

Haut de page

Retour	Droites et points
Suite	Médianes concourantes – Démonstrations Illustration en 3D du centre de gravité d'un triangle Construire le triangle connaissant les médianes Quatre triangles Triangles et carrés Triangles et droites de partage Triangle médian
Voir	DicoMot DicoNombre Droite de Simson Droite d'Euler Éléments de géométrie	Triangle – Débutants, novices Médianes – Glossaire Triangle – Index Cercle Losange et son cercle inscrit
Sites	Médianes – Wikipédia Encyclopedia of triangle centers (ETC) – Tous les centres du triangle possibles et imaginables (plus de 400!) Vergessene Sätze am Dreieck (Teil 2) – Matroids Matheplanet Théorème de Stewart – Wikipédia
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/Mediane0.htm

Haut de page

Renvois de liens

Médianes et partage >>>

Triangles de même aire >>>

Proportion 2 : 1 >>>