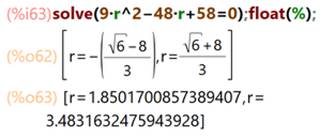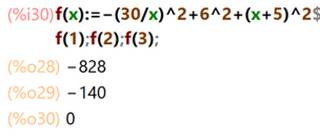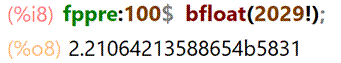|
|||||||||||||||||||||||||||||||||||||
![]()
|
MAXIMA - Logiciel de calcul
formel Théorie des nombres Programmation Logiciel de calcul formel, classé dans la catégorie
des Computer Algebra System (CAS). Logiciel gratuit du même type que les logiciels commerciaux
comme Maple et Mathematica. Applications classiques en calcul sur les
polynômes, calcul sur les matrices, dérivations, intégration . . .
Appréciable pour les étudiants des lycées et d’universités. C’est aussi langage de programmation utile pour
réaliser des recherches sur les nombres. Ce que nous allons découvrir sur ces
pages. |
Voir Liste des programmes réalisés avec Maxima
en index général
|
|
|||
|
Avertissement |
Les signes et conventions utilisées par Maxima différent de ceux
employés par Maple. Source de confusion pour les habituées de l’un des
logiciels pour passer à l’autre. Soyez vigilants. |
||
|
; $ |
Fin de commande avec exécution ( ;) visible
ou non ($). |
||
|
(...
, ...) |
Les instructions à exécuter après do (boucle) ou
then (condition) ou block (fonction) sont mises entre parenthèses et séparées
par une virgule. |
||
|
: := |
Affectation d’une valeur à une variable. Définition d’une fonction. |
||
|
% %pi,
%e |
Dernier résultat de calcul. Constantes Pi et constante e |
||
|
|
Exemple de conversion d’une constante (le nombre
d’or) en son développement décimal. |
||
|
%
i 12 %
o 13 |
Numérote les entrées (input) et les sorties
(output) du programme : ici, input numéro 12 et sortie numéro 13. |
||
|
a*b |
Signe de la multiplication, obligatoire. |
||
|
a^b
ou a**b |
a porté à la puissance b |
||
|
a
# b |
a différent de b ; tous les autres signes
sont classiques. |
||
|
sqrt(a)
ou a^(1/2) |
Racine carrée de a. |
||
|
Integerp primep |
Test si un nombre est un entier. Test si un nombre est premier. |
||
|
|
Partitions d’un nombre. |
|
|
Quantité de combinaisons et de permutations.
Nécessité de charger (load) le logiciel (functs). |
|
|
Utile à savoir lors de recherche en anglais. |
|
|
Pour
charger le logiciel |
|
|
Commentaire:
/* pour ouvrir le commentaire et |
|
Ctrj-Maj |
Pour
exécuter le programme |
|
expand(%) |
Pour
développer une expression |
|
float(%)
|
Pour
obtenir la valeur décimale d’une expression |
|
|
Pour évaluer une expression : la définir avec deux points égal (:=),
puis donner à x la valeur souhaitée. Si l'on ne veut pas qu'une expression soit évaluée, on
met une apostrophe |
|
makelist
|
Séquence en liste |
|
kill(all)$ |
Réinitialisation de toutes les variables (équivalent de restart dans Maple) |
|
|
Création du produit des diviseurs
des nombres. |
|
|
Sommation des nombres Deux
possibilités. |
|
|
Arrêt de traitement d'une boucle Break n’existe pas mettre return |
|
|
Quantité de chiffres pour les
calculs avec fppre. Expression du nombre en flottant
avec bfloat. |

![]()
Exemples
|
|
||
|
|
Calcul de la somme d’une fonction. |
|
|
|
Somme et conversion d’une fraction
en numérique Aussi possible avec bfloat |
|
|
|
Calcul du produit d’une fonction. |
|
|
|
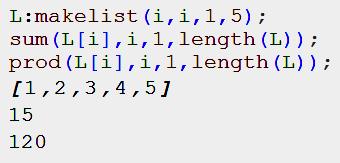
Calcul avec liste de nombres Somme et produit peuvent s’appliquer à une liste.
Voir makelist en rubrique listes. Le crochet permet de sélectionner l’élément dans
la liste. La borne de fin de calcul est égale à la quantité
d’éléments d la liste (length). |
|
|
|
|||
|
Programme de calcul des carrés
On a appris
|
Explications (% i 5) est une notation automatique de Maxima, utile pour repérer le
numéro d’une zone de programmation et du résulta de son calcul. La boucle typique commence par for
(pour), puis définit une variable avec son point de départ i = 1 noté i : 1. Vient ensuite la valeur d’arrivée thru 10
(jusqu’à 10). L’instruction do (faire) suivi de
l’ouverture d’une parenthèse indique le
début du travail dans la boucle. La fin du travail est notifiée par la
fermeture de la parenthèse. Les instructions de travail dans la boucle sont
séparées par une virgule. En l’occurrence le travail consiste à calculer la valeur nommée a en
calculant le carré de la variable de boucle i. Puis, à imprimer (print) les résultats. L’instruction d’impression indiquera la valeur de n et de son carré,
réunis par le texte indiqué dans les guillemets. Le programme se termine par le symbole dollar, indiquant que nous ne
souhaitons pas les intermédiaires de calcul. |
||
|
|
Le même programme qui calcule les carrés des nombres pairs dans l’ordre décroissant. C’est le rôle de l’instruction step (marche d’escalier) qui accepte les valeurs
négatives. Par défaut, le pas de calcul est égal
à +1. |
||
|
|
Trois possibilités pour définir une boucle. |
||
|
|
Calcul des puissances de 2, à rebours, à partir de 1024. Utilisation de l’instruction de boucle while
(tant que). Tant que n est supérieur à 0 poursuivre les calculs. La valeur de n est justement égale
au quotient de n par 2. Valeur qui décroit à chaque itération pour atteindre
2, puis 1 puis 0. Une autre formulation du programme
|
||
|
|
||
|
Programme
On a appris
|
Explications Avec le calcul des factorielles. Ce calcul est mis sous forme de
sous-programme : un module autonome qui pourra être appelé par un autre
programme. Son nom est fact et s’applique au nombre n. Le : = introduit la définition et block indique que la suite comprend plusieurs
instructions qui seront entourées par des parenthèses.
Entre crochets, sont déclarées les variables internes à la procédure.
Ici, une seule [a]. Le programme débute en précisant la valeur de départ de la variable a.
Ici le : veut dire égal. Vient la boucle qui calcule les étapes successives de la factorielle
(1x1 = 1, 1x2 = 2, 2x3 = 6, ...). La valeur est rendu visible à l’extérieur du programme par
l’instruction return. C’est la valeur finale qui sera présente à la sortie de
ce programme. Le symbole $ indique que nous voulons ignorer la cuisine interne du
programme. Le programme d’appel demande la factorielle du nombre 5 ( fact(5) ) et
répond avec la valeur 120. |
|
|
|
||
|
Programme récursif
On a appris
|
Explications La fonction (on dirait procédure avec d’autres
logiciels) est définie par son nom fact (au choix) et par les instructions
qui suivent les symboles := La définition commence par une instruction conditionnelle
classique : if ... then ... else …. (si ... alors ... sinon....) Si n est inférieur à 1, la factorielle vaut 1
sinon elle vaut le produit de n avec la factorielle précédente (n – 1). L’appel à la fonction dans la définition de la
fonction est une capacité des logiciels dits récursifs. Le symbole dollar
indique que le programme est terminé et que son exécution sera cachée. |
|
|
Programme itératif
On a appris
|
Explications Cette fois la fonction (procédure) est définie
par un ensemble d’instructions regroupées dans un block. Les variables locales sont déclarées entre crochets (ici une variable temporaire de calcul
m). La variable temporaire m est mise à 1. Lancement d’une boucle de calculs avec while (tant que) qui va tourner tant que n
n’atteint pas 0. Le calcul dans la boucle commence par do ( et se termine par la fermeture de la parenthèse, les instructions sont déparées par
une virgule. Deux instructions dans la boucle : calcul de
n*m, le produit étant placé dans m. Puis décrémentation de n. La valeur de n
va progressivement se diriger vers 0. Derrière la boucle, la valeur de m est rappelée,
car c’est elle qui contient la valeur calculée de la factorielle et c’est
elle qui sera visible par le programme appelant. Justement le programme appelant demande la factorielle
de 10. |
|
Voir Factorielle – Programmation
expliquée pas à pas
|
|
||
|
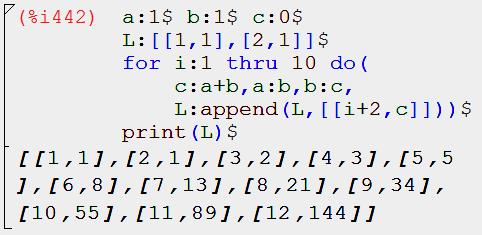
Programme
|
Explications Ce programme établit la liste des nombres
de Fibonacci avec indication de leur rang. La liste l est initialisée avec les deux premiers
couples de valeurs. Le nouveau nombre c est ajouté à la liste en
utilisant l’instruction append (apposer). La manipulation des listes sera expliquée sur une
autre page dédiée. |
|
|
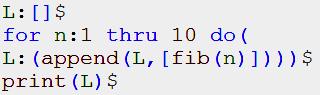
Appel direct à la fonction Fibonacci
|
Maxima dispose d’une instruction (fib)
donnant directement le énième nombre de Fibonacci. |
|
|
|
Création du produit des diviseurs
des nombres. |
![]()
|
Retour |
|
|
Suite |
|
|
Sites |
|
|
Cette page |
![]()