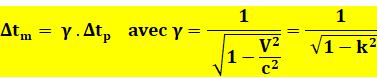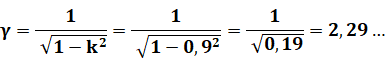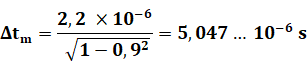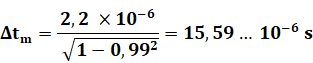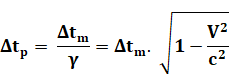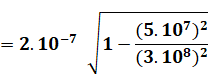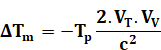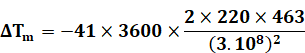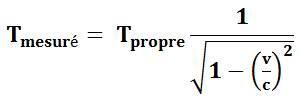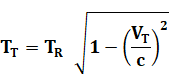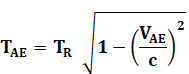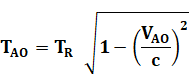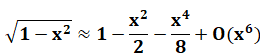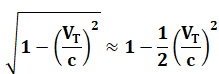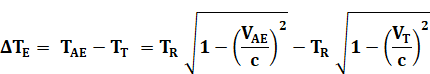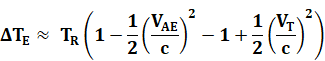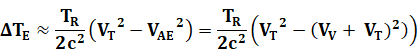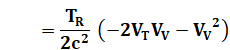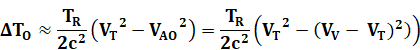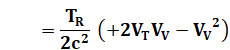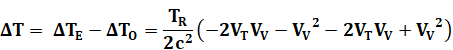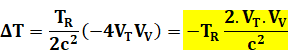relativité calcul du temps relatif

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/11/2017 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	PHYSIQUE
Débutants Général	RELATIVITÉ				Glossaire Général
INDEX Sciences Einstein Galilée	Débutant		Approche	Concepts modernes
	Restreinte		Générale	Matière-énergie (E = m.c²)
	Historique		Temps relatif	Preuves
	Formule		Jumeaux	EPR
	Calculs
	Terminale	Sommaire de cette page >>> Vitesses relatives >>> Image de la porte >>> Particule >>> Expérience des deux avions >>> Établissement de la relation

CALCUL du Temps Relatif

La relativité restreinte dit que, pour des vitesses très élevées, les durées ne sont pas perçues de la même manière selon que:

vous êtes associé à l'événement, ou que

vous êtes de passage à grande vitesse.

Et que dire d'un observateur face à deux phénomènes mobiles se déroulant sous ses yeux?

Rappel de la formule de calcul et exemples des calculs mettant en évidence deux difficultés souvent rencontrées par les étudiants de terminale:

la notion de référentiels en mouvement les uns par rapport aux autres, et

la technique opératoire de l'algèbre (une fois de plus!).

Vitesses relatives
Postulat d'Einstein (1905)	La vitesse de la lumière dans le vide est la même dans tous les référentiels galiléens. C'est une constante fondamentale de la physique. Elle ne dépend ni du mouvement de la source, ni de celui de l'observateur. Remarques Galiléen précise simplement que ce référentiel (cette "bulle") est au repos ou en mouvement rectiligne uniforme et non pas en accélération. Un cadre sympathique pour les calculs! La lumière est une onde électromagnétique est on dit plutôt célérité que vitesse.
Durée propre	La durée propre est le temps qui sépare deux événements survenant au même endroit dans le même référentiel. Notation: (delta t_p , avec un p comme propre) Exemple: je mesure 10 minutes entre l'arrêt du train et son départ.
Mouvement rapide!	Le train est dans son référentiel (sa "bulle"). Un observateur se trouve dans un autre référentiel en mouvement (une autre "bulle", en mouvement, celle-ci) à la vitesse V. Sa perception du temps est différente. Lui mesurera un écart de temps entre arrêt et départ du train de delta t_m (avec un m comme mesurée ou mouvement): La théorie de la relativité restreinte donne la relation entre ces deux durées: c est la célérité de la lumière; k est le rapport des vitesses Voir Pourquoi cette formule?
Exemple	L'observateur passe devant le train à la vitesse V = 0,9 c. Notez tout de suite que cela est fictif. Aucune fusée ne peut atteindre une telle vitesse. Pour l'observateur les 10 minutes du train sur Terre deviendront: 10 x 2,29 = 22,9 minutes Le temps lui semble plus long sur Terre, ou plus court chez lui.

Image de la porte entrebâillée

Dans l'espace-temps, la durée est une dimension comme les trois autres de l'espace. Imaginez que cette dimension-temps soit l'équivalent de la largeur apparente d'une porte. Imaginez que selon la vitesse à laquelle vous l'observez, la porte soit fermée (V = 0) ou entrebâillée (V) ou ouverte (V = c). La taille apparente de la porte varie selon la vitesse, comme la dimension-durée varie avec la vitesse.

Autre idée: théorème de Pythagore et sa généralisation (Minkowski):

Plan: x² + y² = H²;

Espace: x² + y² + z² = H²;

Espace-temps: x² + y² + z² - ct² = H². Le temps contribue à la relation.

Hermann Minkowski (1864-1909), reprend les idées d'Henri Poincaré (1854-1912) et celles de Hendrik Lorentz (1853-1928). Il constate que les transformations de Lorentz sont plus simples en faisant l'hypothèse que l'espace et le temps ne sont pas des entités distinctes. Elles forment un tout à quatre dimensions.

Les distances sont évaluées en tenant compte des distances spatiales et des durées qui les séparent dans le temps. Une distance entre deux personnes est donc égale par la distance habituelle à laquelle il faut soustraire, en gros, le temps qu'il faut à la lumière pour aller d'une personne à l'autre (Voir la relation exacte).

Voir Projections / Lumière des étoiles

Particule 1 (Muon) – Simple application de la relation
Durée de vie au repos: (de sa naissance à sa désintégration)	dans le référentiel lié au muon.
Vitesse du muon dans le laboratoire:	0,9 c dans le référentiel du laboratoire.
Durée "dilatée vue" du laboratoire:
Si on utilise un accélérateur qui propulse le muon à 0,99c, la durée est encore plus dilatée:

Particule 2 – Application de la relation à l'envers
Parcours d'une particule dans le labo.	d = 10 m
Vitesse	V = 10 / 2 . 10^-7 = 5 . 10⁷ m.s^-1
Durée propre: Sans changement perceptible. Car la vitesse relative est faible: 0,15% de celle de la lumière. Un calcul plus fin donne: 0,199999999999981 . 10^-6	= 2 . 10^-7 s

Expérience des deux avions – Hafele-Keating (1971)
Deux avions qui font deux fois le tour de la Terre, l'un vers l'est, dans le sens de rotation de la Terre, et l'autre vers l'ouest. Vitesses de vol identiques (V_V). Durée du vol: 41,0 h Horloges atomiques (ultra-précises) à bord et une autre au sol. Elles permettent de constater: Soit un écart total de (avec la précision de mesure):
Visualisation et notations
Théorie de la relativité donne cette relation: écart sur la durée mesurée durée propre du vol, V_T vitesse de la surface de la Terre dans un référentiel de référence (expliqué ci-dessous). V_V vitesse de vol des avions dans ce même référentiel.
Vitesse avion faible par rapport à celle de la lumière. Effet de la relativité restreinte faible. Écart entre la durée propre et la durée mesurée faible.		Aucun effet observable par les passagers des avions.
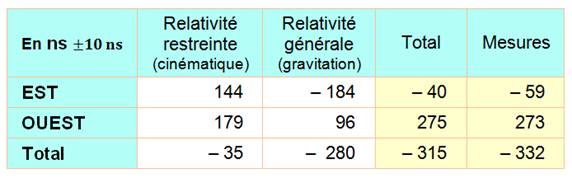
Calcul et comparaison V_Vol = 220 m.s^-1 V_Terre_(équateur) = 463 m.s^-1 T_P = 41,0 h c = 3 . 10⁸ m.s^-1	L'expérience à donné: 332 17 ns soit de 315 à 349 ns. La mesure est conforme aux résultats du calcul.

Établissement de la relation
Rappel numérique Mesure de l'écart de temps témoignant du fait que les horloges à bord des avions ralentissent.
Écart de temps total mesuré (avec la précision).
Formulation Écart de temps à l'est = temps de vol avion à l'est moins temps de vol vu de la Terre. Écart de temps à l'ouest = temps de vol avion à l'ouest moins temps de vol vu de la Terre.
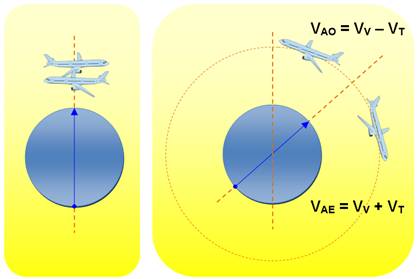
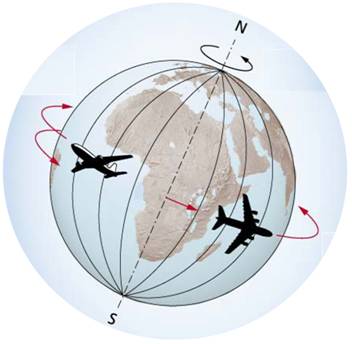
Relation entre vitesses. Composition classique des vitesses. Plus ou moins selon le sens de l'avion.	La Terre tourne d'ouest en est (le contraire du mouvement apparent du Soleil). Au bout d'un certain temps, l'avion allant vers l'est profite de la vitesse de la Terre qui l'emporte avec elle. Au départ, cet avion avait déjà une vitesse Terre. L'autre, une vitesse Terre négative.

Nous allons maintenant appliquer la relation classique de la relativité (facteur de Lorenz). Nous sommes en présence de deux types de mouvements: avions et Terre. Deux référentiels sont nécessaires. L'astuce pour réaliser les calculs consiste à imaginer un observateur externe qui regarde tout cela dans sa "bulle", soit un référentiel supplémentaire, un référentiel de référence (centre de la terre, par exemple). Hormis cela, le reste est du calcul.
Trois référentiels galiléens.		Référentiel Avion Référentiel Terre Référentiel de référence
Relation entre temps pour la Terre et pour les avions en fonction du temps dans le référentiel de référence. Attention: relation inversée par rapport à la relation classique, car on cherche le temps propre à partir du temps mesuré:
Développement limité utilisé pour linéariser la racine avec x petit (On profite du fait que la vitesse avion ou Terre est petite devant la vitesse de la lumière pour utiliser une approximation)
Application en ne conservant que le terme en x².
Retour à notre formule avec l'avion de l'est
Même chose pour l'ouest
Écart complet