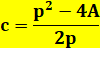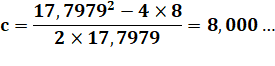NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 09/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Résolution				Glossaire Triangle
INDEX Triangle rectangle Triangle	Résolution	Formules	Hauteur	Aire (Héron)
	Hypoténuse	Longueur de corde	Projection	T 13 14 15
	Triangle Rectangle – Cas classiques		Triangle Rectangle – Cas spéciaux
		Sommaire de cette page >>> Construction – Hypoténuse et hauteur >>> Calculs – Hypoténuse et hauteur >>> Calculs – Hypoténuse et périmètre >>> Calculs – Aire et périmètre >>> Résolution pieds de hauteur

TRIANGLES RECTANGLES

Résolution de cas spéciaux

Hauteur, aire, périmètre

La résolution du triangle rectangle dans les cas classiques est relativement simple. On trouvera la résolution du triangle rectangle comme cas particulier du triangle quelconque en index de résolution du triangle.

Ici, on aborde les cas plus complexes où on ne connait que l'hypoténuse et la hauteur correspondante ou encore le périmètre et l'aire. L'équation du deuxième degré va venir à notre secours.

Construction – Hypoténuse et hauteur
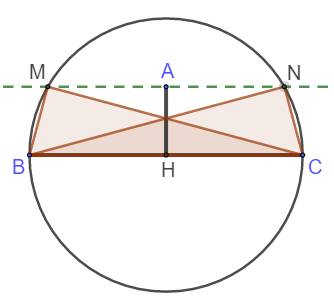
But Construire un triangle rectangle dont on connait la longueur de l'hypoténuse (BC) et celle de la hauteur (AH). Construction Construire le segment BC. Construire un segment perpendiculaire à BC de longueur AH (n'importe où). Perpendiculaire en A à AH Cercle de diamètre BC. Intersections M et N Les triangles BMC et BNC sont les triangles rectangles recherchés.

Calculs – Hypoténuse et hauteur
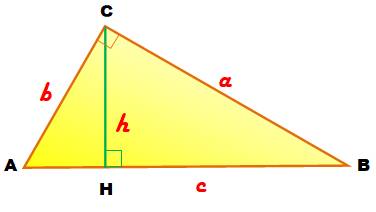
But Calculer la longueur des côtés connaissant la longueur de l'hypoténuse (c) et celle de la hauteur (h). Remarque Avec c et h, on connait l'aire du triangle rectangle: A = 1/2 ch = 1/2 ab
Calculs Avec le théorème de Pythagore:	c² = a² + b²	b² = c² – a²
Avec l'aire:	A = 1/2 ab	4A² = a² b²
En éliminant b:	4A² = a² (c² – a²)
Sous forme d'équation (c et A sont connus):	a^4 – c²a² + 4A² = 0
Exemple numérique c = 8 et h = 2 => A = 8 On pose x = a²	x² – 64x + 256 = 0
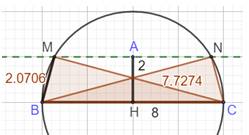
Les solutions, confirmées par construction avec GeoGebra:	a = 2,07055 … & b = 7, 7274 …

Voir Longueur d'une corde entre deux triangles rectangles

Calculs – Hypoténuse et périmètre
Avec les mêmes notations. p et c sont connus.	p = a + b + c b = (p – c) – a = k – a
En reprenant la relation de Pythagore:	c² = a² + (k – a)² = 2a² – 2 ka + k²
Équation (k et c sont connus):	2a² – 2 ka + k² – c² = 0
Longueur de l'autre côté:	b = p – c – a Il se trouve que c'est aussi la seconde solution de l'équation.
Exemple numérique c = 8 et p = 17,7979 => k = p – c = 9,7979	2a² – 19,6a + 9,8² – 8² = 0
Solutions:	b = 7,7274… et a = 2,0705…

Calculs – Aire et périmètre
Avec les mêmes notations. A et p sont connus.	c² = a² + b² A = 1/2ab => 4A = 2ab
Identification de carrés:	a² + b² + 2ab = (a + b)² = c² + 4A a² + b² – 2ab = (a – b)² = c² – 4A
Avec le périmètre:	a + b = p – c (a + b)² = c² + 4A = (p – c)²
En équation, c est l'inconnue:	2pc – p² + 4A = 0
On connait alors l'hypoténuse et le périmètre:	Voir le cas précédent pour calculer a et b.
Exemple numérique A = 8 et p = 17,7979

Voir Calculs de la longueur des côtés

Résolution avec pieds de hauteur		haut
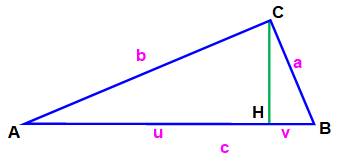
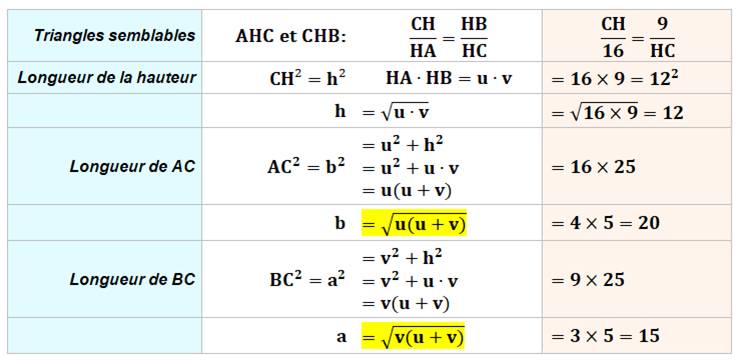
Cas de résolution Segments découpés par la hauteur issue de l'angle droit. Question Un triangle rectangle ABC et sa hauteur CH. On ne connait que u et v. Est-il possible de résoudre le triangle: connaitre ses côtés a, b et c ? Solution Prenons u = 16 et v = 9, par exemple. Et constatons que les triangles rectangles AHC et CHB sont semblables.
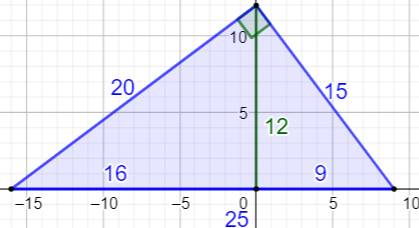
Calculs Figure de confirmation

Voir Brève 52-1033

Suite	Triangle rectangle Triangles – Formules Triangle – Résolution Rayon du cercle inscrit
Voir	Triangles héroniens Triangle – Introduction Triangle – Index Volume du tétraèdre Formule de Héron pour le trapèze
Sites
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/ResTRect.htm