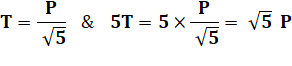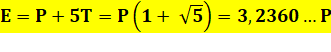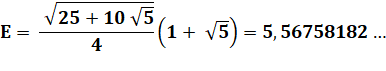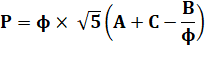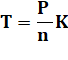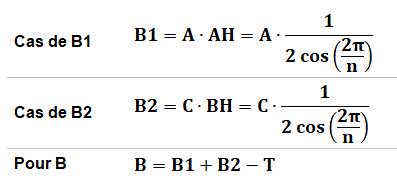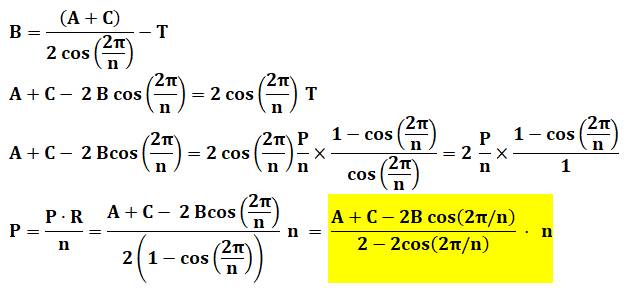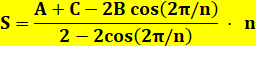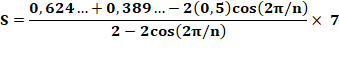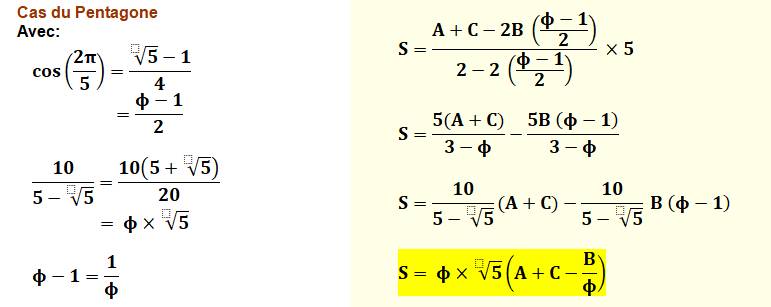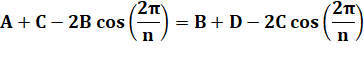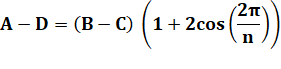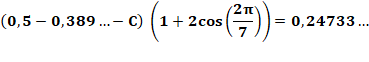|
Édition du: 15/07/2022 |
|
INDEX |
PENTAGONES |
||
|
Mesures – Formules |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
à cinq branches Quelle
est la relation entre l'aire de l'étoile à cinq branches avec le pentagone
central ? Occasion de
résoudre un défi géométrique réputé difficile. Puis,
généralisation au polygone régulier à n côtés. |
||
|
|
Sommaire de cette page >>> Aire de l'étoile et aire du pentagone >>> Aire d'une branche de l'étoile >>> Défi des trois triangles dans le pentagone >>> Généralisation au polygone >>> Aire du polygone via des triangles >>> Aire du polygone appliquée au pentagone >>> Avec quatre triangles – Comparaison |
Débutants Glossaire |
|
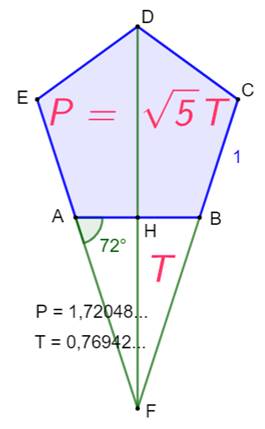
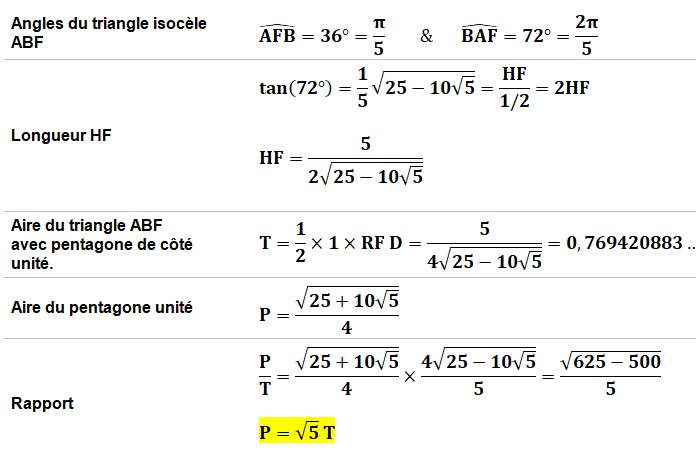
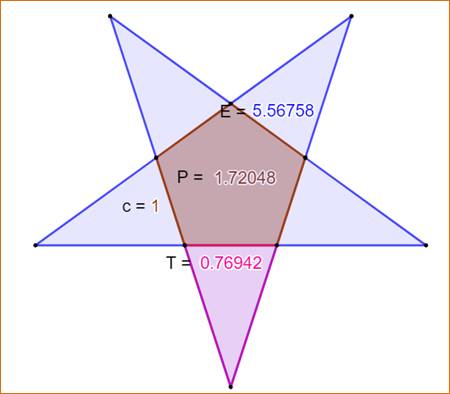
Construction Un pentagone
ABCDE de côté unité dont l'aire est P. La branche de
l'étoile ABF dont l'aire est T. Propriété L'aire du
pentagone vaut racine de 5 fois l'aire de la branche (démonstration
ci—dessous).
Aire de l'étoile en fonction de
l'aire du pentagone (unité)
Formule complète pour l'aire de
l'étoile (pentagone unité)
Valeur à multiplier par c² pour un pentagone régulier
de côté c. |
Pentagone unité avec une branche de
l'étoile
|
|
Aire de l'étoile (E), du
pentagone unité (P) et d'un triangle (T)
|
Conseil: pour suivre la démo, faire une capture d'écran de la figure pour
l'avoir sous les yeux en même temps que ce tableau.
|
|
|
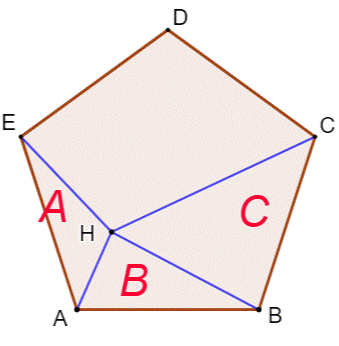
Construction Un pentagone
ABCDE. Aire notée P. Un point interne
H quelconque. Les aires des
trois triangles A, B et C sont données. Propriété Démontrer que (avec phi le nombre
d'or): Commentaires Ce défi a été posé par
l'internaute EylemGercek,
connu pour ses énigmes mathématiques avancées. Sa solution m'a été communiquée par MonGuy. Notez cette superbe intuition qui consiste à
considérer la branche ABF de l'étoile. |
|
|
|
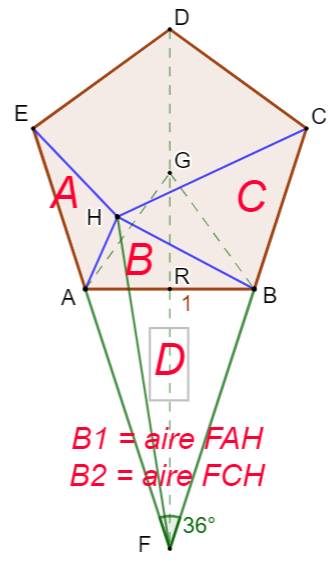
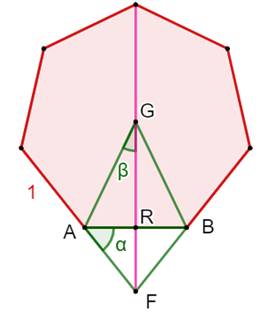
Construction La branche ABF de l'étoile. On note D l'aire de la branche. On note B1 et B2 l'aire des triangles AHF et BHF
qui, à eux deux couvrent B et D. Démonstration Il s'agit de comparer B1 et B2, respectivement à
A et C. Les triangles A et B1 ont le même sommet et leur
base est située sur la même droite. Les aires sont proportionnelles à la
longueur des bases. Voir la suite du calcul dans le tableau
ci-dessous. |
|
|
|
|
||
Voir Angle
et nombre d'or / Démonstration
du théorème de Pythagore par Euclide
|
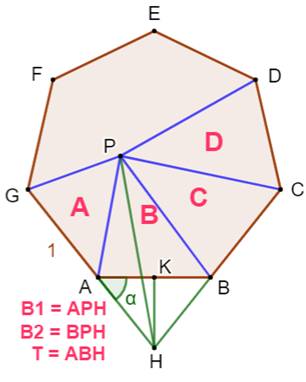
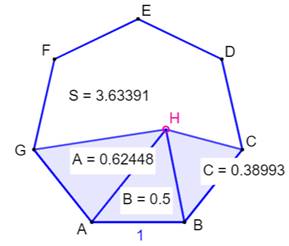
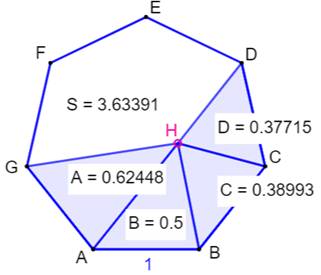
But Un polygone régulier (ici un heptagone): aire P. Sa branche ABF: aire T Exprimer T en fonction de P. On utilisera le rapport K entre l'aire du
triangle ABG et le triangle ABF (T) Aire de la branche T en fonction de
celle du polygone
|
Heptagone avec une branche
Valeurs numériques pour l'heptagone unité: AB = 1 K = 1,65597 A(ABH) = 0,31349; A(ABP) = 0,51913 A(Polygone) = 3,63391 |
|
Voir Angles
des polygones
|
Avec le point P quelconque Calcul semblable à celui du pentagone.
Le polygone étant régulier, l'aire du triangle T
est une constante quelle que soit la branche. |
|
|
|
|
||
![]()
Compléments
|
La formule générale pour le polygone régulier
peut être appliquée au pentagone régulier. Évidemment, on doit retrouver la formule
vue ci-dessus. |
Voir Exemple numérique Voir Formules
de l'aire des polygones réguliers |
||
|
RAPPEL: formule des trois triangles Aire calculée avec la connaissance de l'aire de
trois triangles issus d'un même point quelconque P et reposant sur trois
côtés contigus du polygone.
Exemple (Voir
figure)
|
|
||
|
|
|||
|
Avec quatre triangles, il est possible d'évaluer
l'aire de deux manières: avec A, B et C ou avec B, C ou D. Dans les deux cas, le dénominateur est le même,
si bien que l'égalité s'exprime ainsi:
Exemple (Voir
figure)
|
|
|
Merci
à MonGuy pour l'idée de cette page et pour sa solution de
l'énigme
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/EtoiAire.htm
|