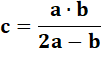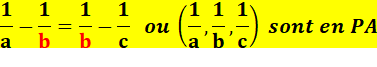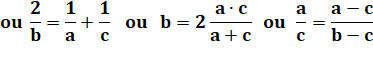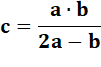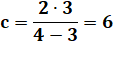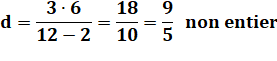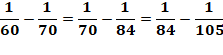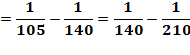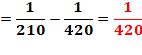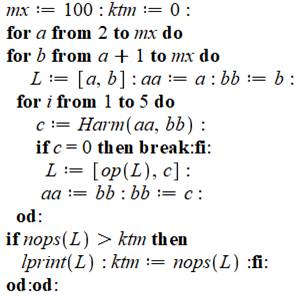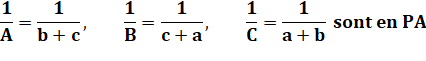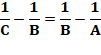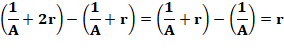|
|||||||||||||||||||||||||||||||||||||||||
|
SUITE
HARMONIQUE ou PROGRESSION
HARMONIQUE Nombres successifs tels que chacun des triplets (a, b, c) de
la suite satisfait la relation:
PA:
Progression Arithmétique
|
Anglais: Harmonic progression
Voir Moyenne
harmonique / Suite et Série
|
|
|||||
|
Quelques suites d'entiers en PH Connaissant
a et b, calcul de c:
|
Exemple avec 2, 3, 6, limitée à 6.
|
||||
|
Triplets
et + |
Quadruplets
et + |
Quintuplets
et + |
|||
|
[2, 3, 6] [3, 4, 6, 12] [3, 5, 15] [4, 6, 12] [4, 7, 28] [5, 8, 20] [5, 9, 45] [6, 8, 12, 24] [6, 9, 18] [6, 10, 30] [6, 11, 66] [7, 12, 42] [7, 13, 91] [8, 12, 24] [8, 14, 56] [8, 15, 120] [9, 12, 18, 36] [9, 15, 45] [9, 16, 72] [9, 17, 153] [10, 12, 15, 20, 30, 60] [10, 15, 30] [10, 16, 40] [10, 18, 90] [10, 19, 190] |
[3, 4, 6, 12] [6, 8, 12, 24] [9, 12, 18, 36] [10, 12, 15, 20, 30, 60] [12, 15, 20, 30, 60] [12, 16, 24, 48] [14, 20, 35, 140] [15, 20, 30, 60] [15, 21, 35, 105] [18, 24, 36, 72] [20, 24, 30, 40, 60, 120] [21, 28, 42, 84] [24, 30, 40, 60, 120] [24, 32, 48, 96] [27, 36, 54, 108] [28, 40, 70, 280] [30, 36, 45, 60, 90, 180] [30, 40, 60, 120] [30, 42, 70, 210] [33, 44, 66, 132] [33, 48, 88, 528] [35, 45, 63, 105, 315] [36, 45, 60, 90, 180] [36, 48, 72, 144] [40, 48, 60, 80, 120, 240] |
[10, 12, 15, 20, 30, 60] [12, 15, 20, 30, 60] [20, 24, 30, 40, 60, 120] [24, 30, 40, 60, 120] [30, 36, 45, 60, 90, 180] [35, 45, 63, 105, 315] [36, 45, 60, 90, 180] [40, 48, 60, 80, 120, 240] [48, 60, 80, 120, 240] [50, 60, 75, 100, 150, 300] [60, 70, 84, 105, 140, 210, 420] [60, 72, 90, 120, 180, 360] [60, 75, 100, 150, 300] [70, 84, 105, 140, 210, 420] [70, 90, 126, 210, 630] [72, 90, 120, 180, 360] [80, 96, 120, 160, 240, 480] [84, 105, 140, 210, 420] [90, 108, 135, 180, 270, 540] [96, 120, 160, 240, 480] [100, 120, 150, 200, 300, 600] [105, 120, 140, 168, 210, 280, 420] [105, 135, 189, 315, 945] [108, 135, 180, 270, 540] [110, 132, 165, 220, 330, 660] [120, 140, 168, 210, 280, 420, 840] [120, 144, 180, 240, 360, 720] [120, 150, 200, 300, 600] |
|||
|
Exemple développé de chaine
harmonique
Remarque importante Tous les inverses des nombres de cette suite sont
en progression arithmétique de raison 1/420 (Voire théorème) Ex: 1/60 – 1/420
= 1/70 1/70 – 1/420 = 1/84 |
Chaines harmoniques les plus grandes (records) [2, 3, 6] [3, 4, 6, 12] [10, 12, 15, 20, 30, 60] [60, 70, 84, 105, 140, 210, 420] [105, 120, 140, 168, 210, 280, 420, 840] [252, 280, 315, 360, 420, 504, 630, 840, 1260, 2520] [2310, 2520, 2772, 3080, 3465, 3960, 4620, 5544,
6930, 9240, 13860, 27720] Fin jusqu'à 1 000 000. Observations Les quatre premières suites ne comportent que des diviseurs de 420: 1, 2, 3, 4, 5, 6, 7, 10, 12, 14, 15, 20, 21, 28, 30, 35, 42, 60, 70,
84, 105, 140, 210, 420. Idem pour la suite avec des multiples de 420. |
||||
|
|
Programme de recherche des chaines harmoniques les
plus grandes (Maple) Réinitialisation générale. Procédure qui teste si le terme suivant de la
suite est un entier. Calcul du 3e terme p à partir de n et m en
évitant la division par 0. Si ce terme est entier (integer) et positif, le
nouveau nombre est renvoyé au programme appelant; sinon on retourne 0. Le programme principal commence par préciser
l'ampleur de la recherche (mx = 100 ou au choix). Le compteur de records
(ktm) est initialisé à 0. Exploration jusqu'à mx des deux premiers termes
de la suite (a et b). Initialisation de la suite (L) avec les deux
premières valeurs. On conserve la mémoire de a et b en créant les variables
de travail aa et bb. La profondeur d'exploration (i) est fixée à 5
(exemple). Calcul de c via la procédure qui renvoie un
entier positif en progression harmonique ou alors 0. Si le retour est nul, la chaine est terminée et
on interrompt l'exploration en i (break). La liste est enrichie du nouveau venu et les
termes de la suite progressent d'un cran. Enfin, on imprime le résultat si la liste
comporte plus de termes (nops) que la liste précédente Le résultat du traitement est affiché en bleu. |
Voir Programmation
– Index
|
|
||
|
Les
nombres a², b² et c² sont en PA. Montrez
que les sommes (b + c, c+ a, a + b) sont en PH. Théorème Trois nombres dont les inverses sont en progression arithmétique,
alors ils sont en progression harmonique. 1/a, 1/b, 1/c en PA <=> a, b, c
en PH |
En ajoutant une somme constante aux trois nombres en PA, les trois
nouveaux nombres restent en PA Ajoutons: ab + bc + ca a² => a² + ab + bc +
ca = a (a + c) + b (a + c) = (a + b) (a
+ c) b² => b² + ab + bc +
ca = a (b + c) + b (b + c) = (a + b) (b
+ c) c² => c² + ab + bc +
ca = a (b + c) + c (b + c) = (a + c) (b
+ c) En divisant par (a + b)(b + c)(c + a)
Alors A, B et C sont en PH s'ils satisfont:
Ce qui est le cas:
|
|
|
|
||
|
Entre 7
et 1/6, créer une suite harmonique de 42 termes |
On passe par les inverses en PA (Voir théorème ci-dessus) Le nombre 6 est le 42e terme d'une suite arithmétique dont
le premier terme est 1/7. 6 = 1/7 + 41 r => 41 r = 6 – 1/7 = 41/7 => r = 1/7 Progression arithmétique 1/7, 2/7, 3/7, …, 41/7, 42/7 = 6 Progression harmonique 7, 7/2, 7/3, …7/41, 1/6 |
|
|
Retour |
|
|
Suite |
|
|
|
|
|
Cette page |
