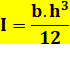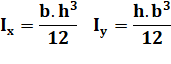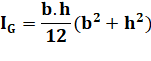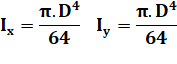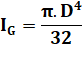|
||||||||||||||||||||||||||||||
![]()
|
|
||
|
|
|
|
|
|
||
|
|
|
|
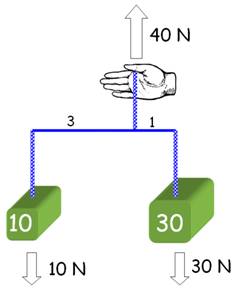
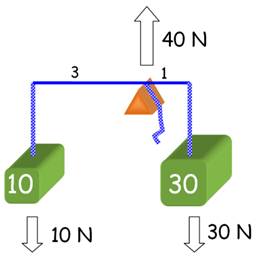
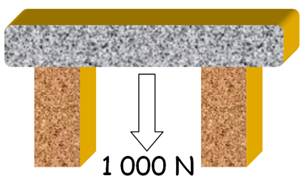
10 x 3 = 30 x 1 |
|
|
|
|
Remarque
|
On
vient de troquer une main contre un pivot pour comprendre la force de
résistance d'un pivot. On
va faire l'inverse, troquer le pivot contre la main, pour comprendre la force
de résistance des supports d'une poutre. |
|
|
||
|
|
|
|
|
|
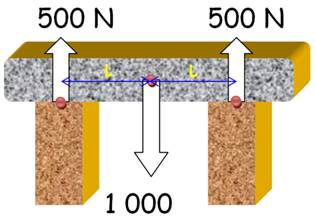
Équilibre de la poutre sur ses supports 500 L = 500
L |
|
|
|
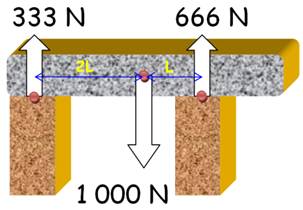
Équilibre de la poutre 333 x 2 L =
666 L |
|
Voir Forces
dans les constructions
|
|
||
|
Capacité d'un élément à section rectangulaire
(poutre) à résister à des efforts de flexion. |
I: moment quadratique (mesure en L4) ou moment d'inertie
(moins recommandé). b: longueur de la base de la poutre h: hauteur de la poutre |
|
|
Notez
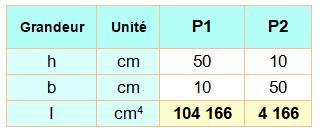
l'influence de la dimension hauteur |
Une poutre résistera d'autant mieux qu'elle sera haute plutôt que
large. L'expérience du double-décimètre en plastique le montre aisément. |
|
|
Ces deux
cas (tableau) illustrent bien l'avantage d'une section plus verticale. |
|
|
|
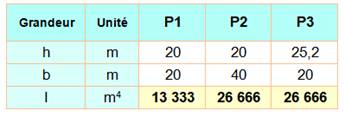
Poutre
carré 20 x 20 cm. On veut
doubler son inertie. Il faut
ajouter soit:
|
|
|
Anglais: Second moment of area or moment of inertia
|
Formules Section
rectangulaire |
|
|
Section
circulaire |
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Livres |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/Support.htm |